Векторное произведение. Координатная форма векторного произведения

Векторным произведением вектора 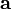на вектор 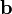в пространстве 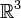называется вектор 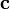, удовлетворяющий следующим требованиям:

§ длина вектора 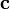равна произведению длин векторов 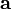и 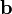на синус угла 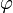; между ними

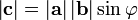
§ вектор 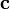ортогонален каждому из векторов 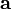и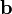

§ вектор 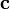направлен так, что тройка векторов 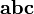является правой.

§ в случае пространства 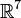требуется ассоциативность тройки векторов .

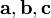Обозначение:

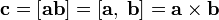
В литературе^[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.

Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.