2015-04-20
757
Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.
Скалярным произведением в векторном пространстве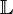 
над полем 
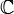называется функция 
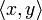для элементов 
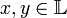, принимающая значения в 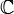, определенная для каждой пары элементов и удовлетворяющая следующим условиям:
1. для любых трех элементов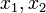 
и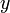 
пространства 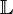и любых чисел 
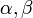справедливо равенство 
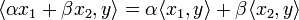(линейность скалярного произведения по первому аргументу);
2. для любых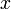 
и 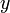справедливо равенство 
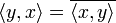, где черта означает комплексное сопряжение (эрмитова симметричность);
3. для любого 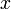имеем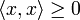 
, причем 
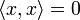только при 
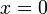(положительная определенность скалярного произведения).
Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.
Заметим, что из п.2 определения следует, что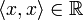 
действительное. Поэтому п.3 имеет смысл несмотря на комплексные (в общем случае) значения скалярного произведения.
