2015-04-20
548
Экстремум — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Определения
Пусть дана функция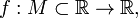 
и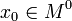 
— внутренняя точка области определения f. Тогда
§ x 0 называется точкой локального максимума функции f, если существует проколотая окрестность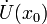 
такая, что
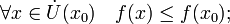
§ x 0 называется точкой локального минимума функции f, если существует проколотая окрестность 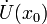такая, что
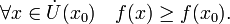
Если неравенства выше строгие, то x 0 называется точкой строгого локального максимума или минимума соответственно.
§ x 0 называется точкой абсолютного (глобального) максимума, если
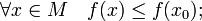
§ x 0 называется точкой абсолютного минимума, если
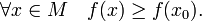
Значение функции f (x 0) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.
[править]Замечание
Функция f, определённая на множестве M, может не иметь на нём ни одного локального или абсолютного экстремума. Например,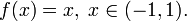 
[править]Необходимые условия существования локальных экстремумов
§ Лемма Ферма. Пусть функция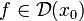 
дифференцируема в точке локального экстремума x 0. Тогда:
.
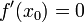§ Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.
[править]Достаточные условия существования локальных экстремумов
§ Пусть функция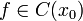 
непрерывна в 
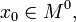и существуют конечные или бесконечные односторонние производные 
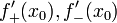. Тогда при условии
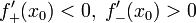
x 0 является точкой строгого локального максимума. А если
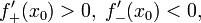
то x 0 является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке x 0
§ Пусть функция f непрерывна и дважды дифференцируема в точке x 0. Тогда при услови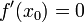и
и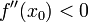 
x 0 является точкой локального максимума. А есл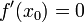и
и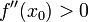 
то x 0 является точкой локального минимума.
