Дифференциал — линейная часть приращения функции.
Обозначения
Обычно дифференциал функции f обозначается df.
Дифференциал в точке x 0 обозначается 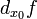 , а иногда
, а иногда 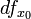 или df [ x 0], а таккже df, если значение x 0 ясно из контекста.
или df [ x 0], а таккже df, если значение x 0 ясно из контекста.
Дифференциал используется в выражении для интеграла 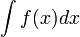 . При этом зачастую дифференциал dx вводится как часть определения интеграла; то есть в определении интеграла обходится определение дифференциала.
. При этом зачастую дифференциал dx вводится как часть определения интеграла; то есть в определении интеграла обходится определение дифференциала.
Также знак дифференциала используется в обозначении Лейбница для производной 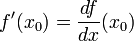 . Это обозначение имеет смысл поскольку для дифференциалов функции f и тождественной функции x верно соотношение
. Это обозначение имеет смысл поскольку для дифференциалов функции f и тождественной функции x верно соотношение
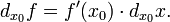
[править] Для функций
Дифференциал функции 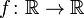 в точке
в точке 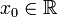 может быть определён как линейная функция
может быть определён как линейная функция
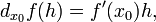
где f '(x 0) обозначает производную f в точке x 0.
Таким образом df есть функция двух аргументов 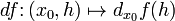 .
.
Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция 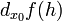 линейно зависящая от h и для которой верно следующее соотношение
линейно зависящая от h и для которой верно следующее соотношение
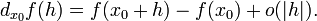
 2015-04-20
2015-04-20 1606
1606
