Признак

У этого термина существуют и другие значения, см. Признак Коши.

ряд

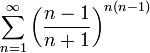
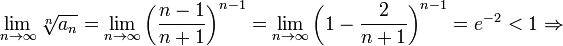ряд сходится.

Радикальный признак Коши — признак сходимости числового ряда:

Если для числового ряда

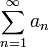
с неотрицательными членами существует такое число d, 0 < d < 1, что, начиная с некоторого номера, выполняется неравенство 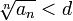, то данный ряд сходится.

Условие радикального признака равносильно следующему:

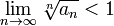
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:

Если для ряда

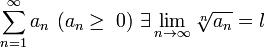, то

если 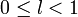ряд сходится,

если l > 1 ряд расходится,

если l = 1 вопрос о сходимости ряда остается открытым.