2015-04-20
510
1. Пусть l < 1. Очевидно, что существует такое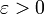 
, что l + ε < 1. Поскольку существует предел 
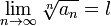, то подставив в определение предела выбранное εполучим:
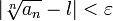
Раскрыв модуль, получаем:
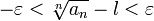
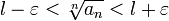
(l − ε) n < an < (l + ε) n
Поскольку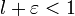 
, то ряд 
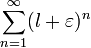сходится. Следовательно, по признаку сравнения ряд 
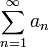тоже сходится.
2. Пусть l > 1. Очевидно, что существует такое 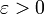, что l − ε > 1. Поскольку существует предел 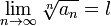, то подставив в определение предела выбранное εполучим:
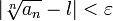
Раскрыв модуль, получаем:
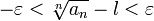
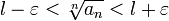
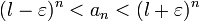
Поскольку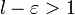 
, то ряд 
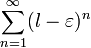расходится. Следовательно, по признаку сравнения ряд 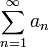тоже расходится.
