2015-04-20
11343
Знакопеременные ряды
Определение 5. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.
Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на – 1.
Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов.
Определение 6. Числовой ряд вида u1-u2+u3-u4+…+ +(- 1 )n- 1. un+ …, где un – модуль члена ряда, называется знакочередующимся числовым рядом.
Теорема 9. (Признак Лейбница )
Если для знакочередующегося числового ряда
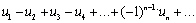(19)
Выполняются два условия:
Члены ряда убывают по модулю u1 > u2 >…> un >…,
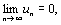
то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n = (u1-u2)+(u3-u4)+…+(u2n-1-u2n).
По условию u1 > u2 >…> u2n-1 > u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n >0 при любом n.
|
|
|
С другой стороны S2n = u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n >0, поэтому S2n < u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный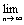 
S2n = S. При этом 0< S ≤ u1.
Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1 = S2n + u2n+1. Перейдём в последнем равенстве к пределу при n→∞: 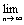S2n+1= 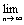S2n+ 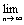u2n+1=S+ 0 =S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому 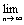Sn = S, то есть данный ряд сходится. Теорема доказана.
Пример.
Исследовать на сходимость ряд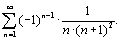 
Применим признак Лейбница.
un =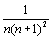 
> un+1 =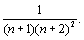 
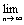un =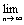 
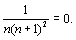
Оба условия признака Лейбница выполняются, следовательно, ряд сходится.
Замечания.
1. Теорема Лейбница справедлива и если условие un>un+ 1 выполняется, начиная с некоторого номера N.
2. Условие un>un+1 не является необходимым. Ряд может сходиться, если оно не выполняется. Например, ряд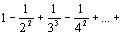 
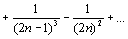сходится, как разность двух сходящихся рядов 
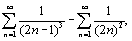хотя условие un>un+1 не выполняется.
Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.
Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.
Пример.
Установить характер сходимости ряда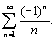 
Очевидно, что данный ряд сходится по признаку Лейбница. Действительно: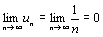 
и un =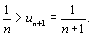 
Ряд, составленный из абсолютных величин членов данного ряда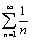 
является расходящимся гармоническим рядом. Поэтому данный ряд сходится условно.
|
|
|
