Определение 18

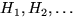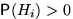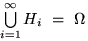Набор попарно несовместных событий таких, что для всех и , называется полной группой событий или разбиением пространства .

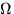События 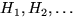, образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события 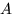могут быть сравнительно просто вычислены (вероятность событию 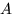произойти при выполнении «гипотезы» ) и собственно (вероятность выполнения «гипотезы» ). Как, используя эти данные, посчитать вероятность события ?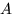

^ Теорема 8 (формула полной вероятности).

Пусть 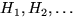— полная группа событий. Тогда вероятность любого события 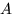может быть вычислена по формуле:

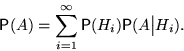
Доказательство.

Заметим, что 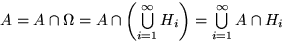, и события 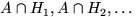попарно несовместны. Поэтому (используем в первом равенстве 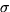-аддитивность вероятностной меры (а что это?), а во втором — теорему умножения)

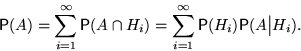
11. формула Байеса:

Пусть 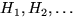— полная группа событий и 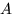— некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие 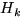, если в результате эксперимента наблюдалось событие 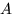, может быть вычислена по формуле:

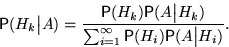
Доказательство.
По определению условной вероятности,

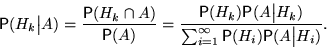
Последнее равенство следует из теоремы умножения и формулы полной вероятности.
Q.D.E.
Пример 19.
Вернемся к примеру 18. Изделие выбирается наудачу из всей произведенной продукции. Рассмотрим три гипотезы: 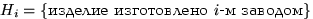, 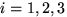. Вероятности этих событий даны: 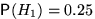, , 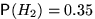. Пусть 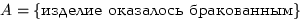. Даны также условные вероятности , , .
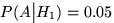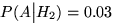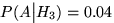Убедиться, что полученные нами вероятности в (а) и (б) совпадают с вероятностями, вычисленными по формуле полной вероятности и формуле Байеса.
Пример 20.
Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0.00001. Можно сделать два предположения об эксперименте: 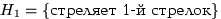и 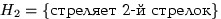. Априорные (a'priori — «до опыта») вероятности этих гипотез одинаковы: .

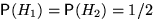Рассмотрим событие . Известно, что

Поэтому вероятность пуле попасть в мишень 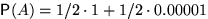. Предположим, что событие 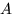произошло. Какова теперь апостериорная (a'posteriori — «после опыта») вероятность каждой из гипотез ?

Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в 100000 раз). Действительно,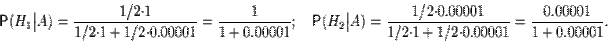

12. Понятие случайной величины и ее задание: Часто в результате испытания происходят события, заключающиеся в том, что некоторая величина принимает одно из своих возможных значений.
В таких случаях удобно вместо множества событий рассматривать одну переменную величину (называемую случайной величиной). Случайная величина обозначается через X, Y, Z, … и т.д.
Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
Пример. В студенческой группе 25 человек. Пусть величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2,…,25.
При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т.е. наступит одно из событий Х = 0, Х = 1, …, Х = 25.
Пример. Измерение курса акции некоторого предприятия. Возможные события заключаются в том, что стоимость акции Y примет некоторое значение в пределах от 0 до ∞.
Пример. Однократное бросание игральной кости. Возможные события заключаются в том, что на верхней грани выпадает Z: 1, 2, 3, 4, 5, 6.
Пример. Подбрасывается монета n раз. Возможные результаты: герб выпал 0, 1, 2, …, n раз.
Различают дискретные и непрерывные случайные величины.
Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной (примеры 3.1, 3.3, 3.4).
Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной (пример 3.2). Заметим, что дискретные и непрерывные величины не исчерпывают все типы случайных величин.
Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называют смешанной.
Очевидно, что для полной характеристики дискретной случайной величины мало знать ее значения. Необходимо им поставить в соответствие вероятности.
Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.
Простейшая формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины (обычно в порядке возрастания) и соответствующие им вероятности:

Х	х 1	х 2	…	хn	…
Р	р 1	р 2	…	рn	…

Такая таблица называется рядом распределения. Допустим, что число возможных значений случайной величины конечно: х ₁, х ₂, …, х_n. При одном испытании случайная величина принимает одно и только одно постоянное значение. Поэтому события Х = х_i (i = 1, 2, …, n) образуют полную группу попарно независимых событий. Следовательно, р ₁ + р ₂ + … + р_n = 1.
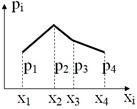
Можно закон распределения изобразить и графически, откладывая на оси абсцисс возможные значения случайной величины, а на оси ординат – соответствующие вероятности. Для большей выразительности полученные точки соединяются прямолинейными отрезками. Получающая при этом фигура называется многоугольником (полигоном) распределения.

13.закон распределение случайной величины:

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее какое именно.

Случайные величины бывают двух типов:
• непрерывные;
• прерывные (дискретные).

Условимся в дальнейшем случайные величины обозначать большими буквами, а их возможные значения – соответствующими малыми буквами.
Пример:
Х- число попаданий при трех выстрелах:
х1 = 0;
х2 = 1;
х3 = 2;
х4 = 3.

Рассмотрим прерывную случайную величину Х с возможными значениями x1, x2, …, xn. Каждое из этих значений возможно, но не достоверно, и величина Х может принять каждое из них с некоторой вероятностью
Х= х1;
Х= х2;
Х= х3;
Х= х4.

Обозначим вероятности этих событий P(X=x1) = p1; P(X=x2) = p2; P(X=xn)=pn.

∑Pm,n = 1, так как несовместные события образуют полную группу. Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если будет задано это распределение, т.е. в точности указано, какой вероятностью обладает каждое из событий. Этим устанавливается так называемый закон распределения случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения прерывной случайной величины Х может быть задан в следующих формах:
• табличной;
• аналитической;
• графической.

Простейшей формой задания закона распределения прерывной случайной величины Х является таблица.

xi	x1	x2	…	xn
pi	p1	p2	…	pn

Такую таблицу называют рядом распределения случайной величины Х.

Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению.

Для непрерывной случайной величины такой характеристики построить нельзя!!!

Для непрерывной случайной величины удобно воспользоваться не вероятностью события Х=х, а вероятностью события Х<х, где х – некоторая текущая переменная. Вероятность этого события, очевидно, зависит от х и есть некоторая функция от х.

Эта функция называется функцией распределения случайной величины Х и обозначается F(х):
F(x) = P(X< x)

Функцию распределения F(x) называют также интегральной функцией распределения или интегральным законом распределения.

Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.

Сформулируем некоторые общие свойства функции распределения:
1.F(x) – неубывающая функция своего аргумента т.е. при x2 > x1 F(x2) > F(x1);
2. F(–∞) = 0;
3. F(+∞) = 1.