Запишем интерполяционный многочлен Лагранжа Ln(x) в другой форме:

где разность 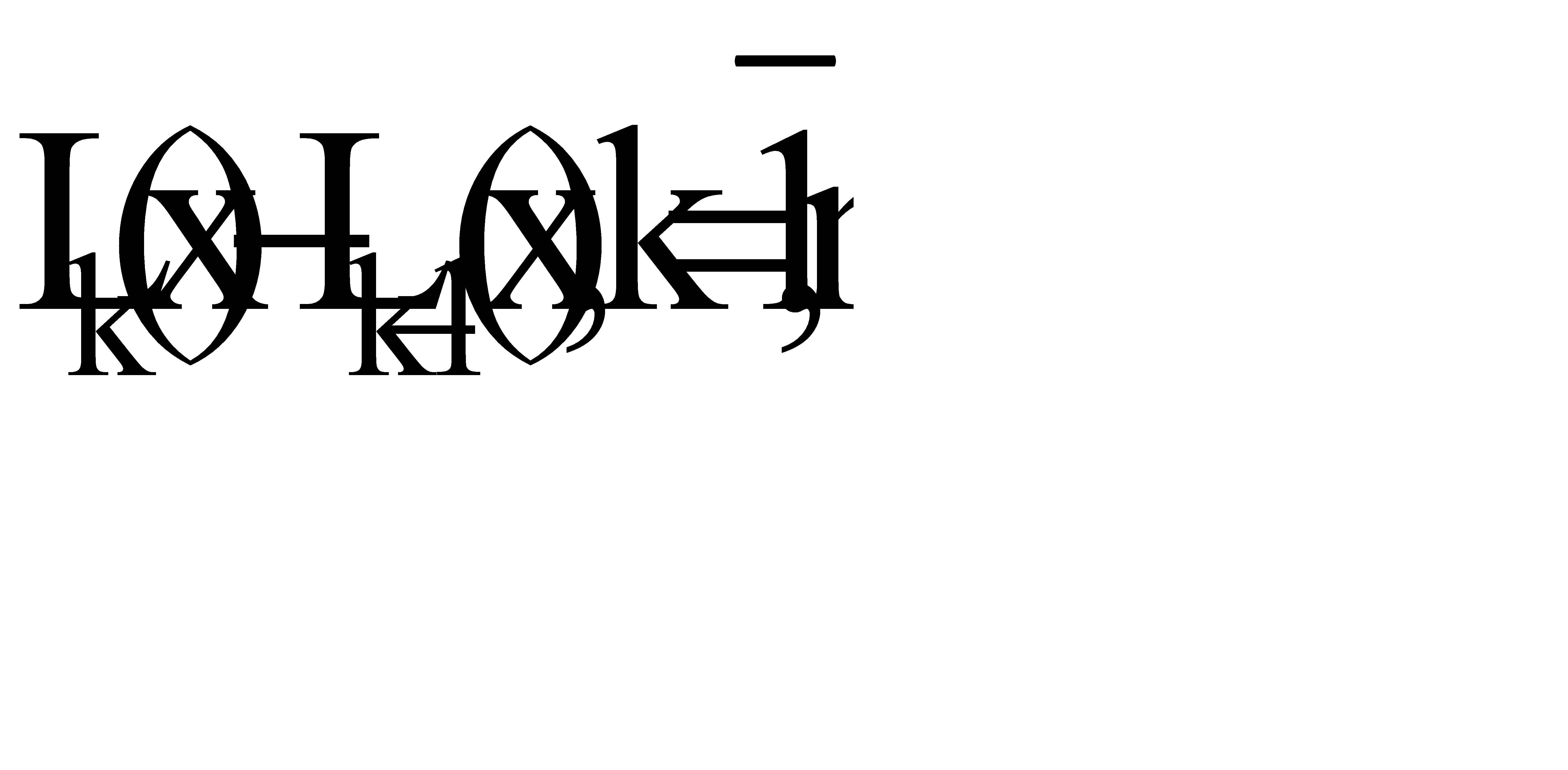 , есть многочлен степени k, обращающийся в нуль в точках x0,¼,xk-1. Поэтому можно записать
, есть многочлен степени k, обращающийся в нуль в точках x0,¼,xk-1. Поэтому можно записать
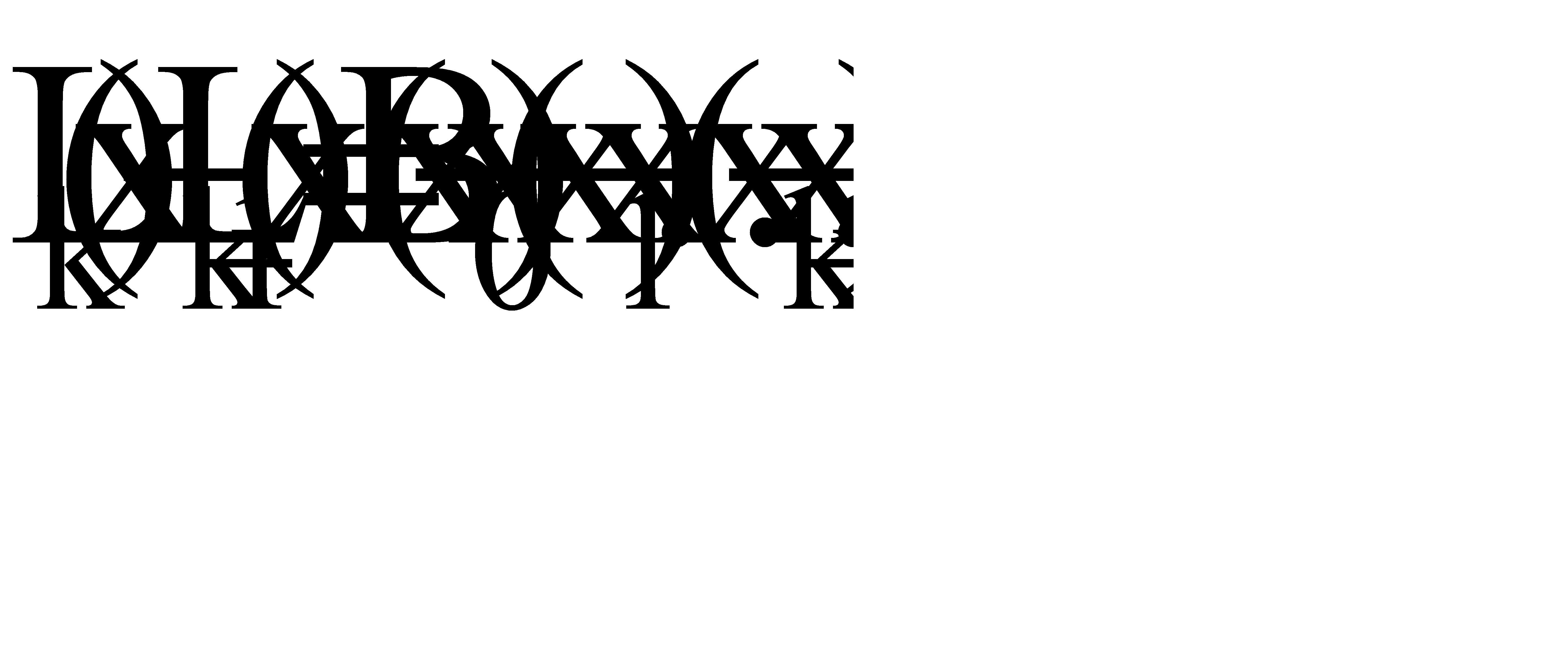
Константу B найдем, полагая x=xk, т.е.
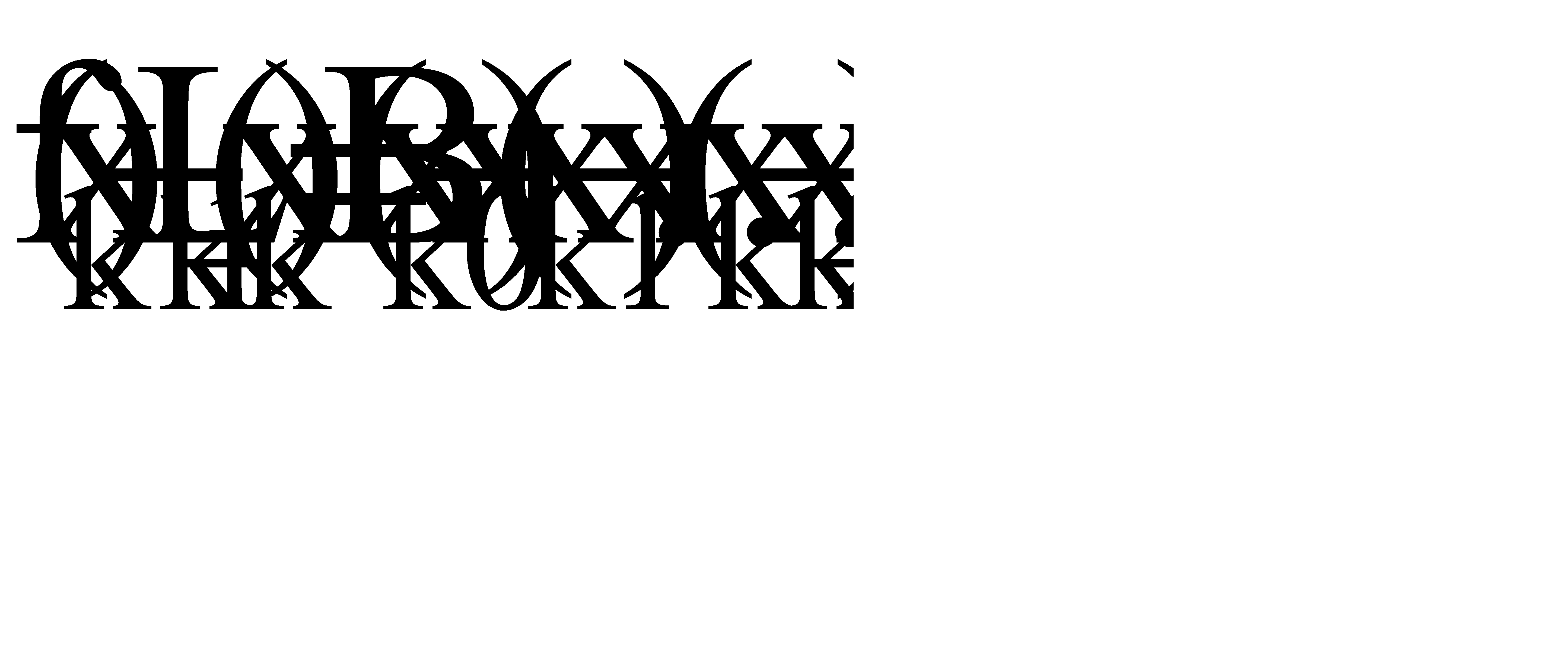 Þ
Þ
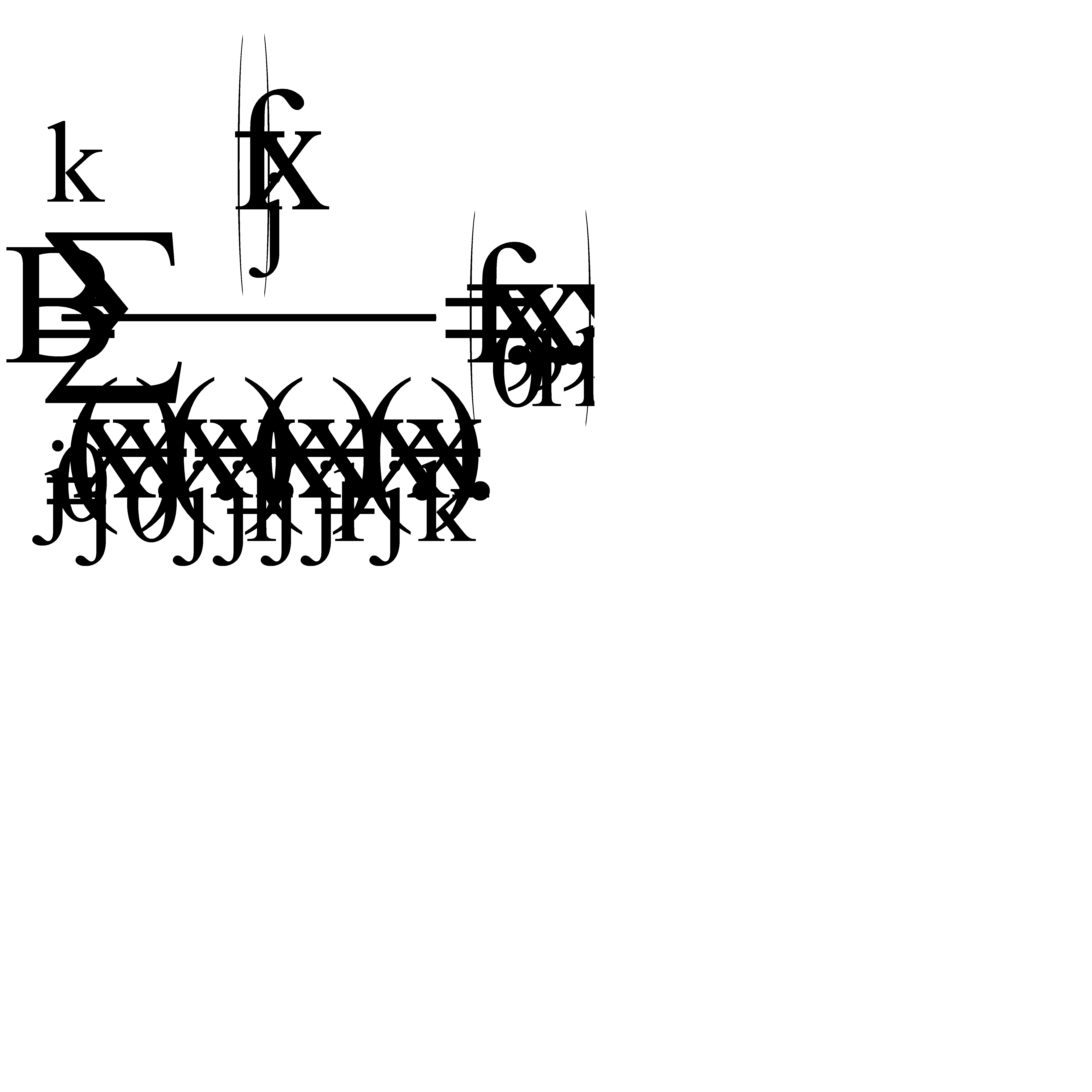
где 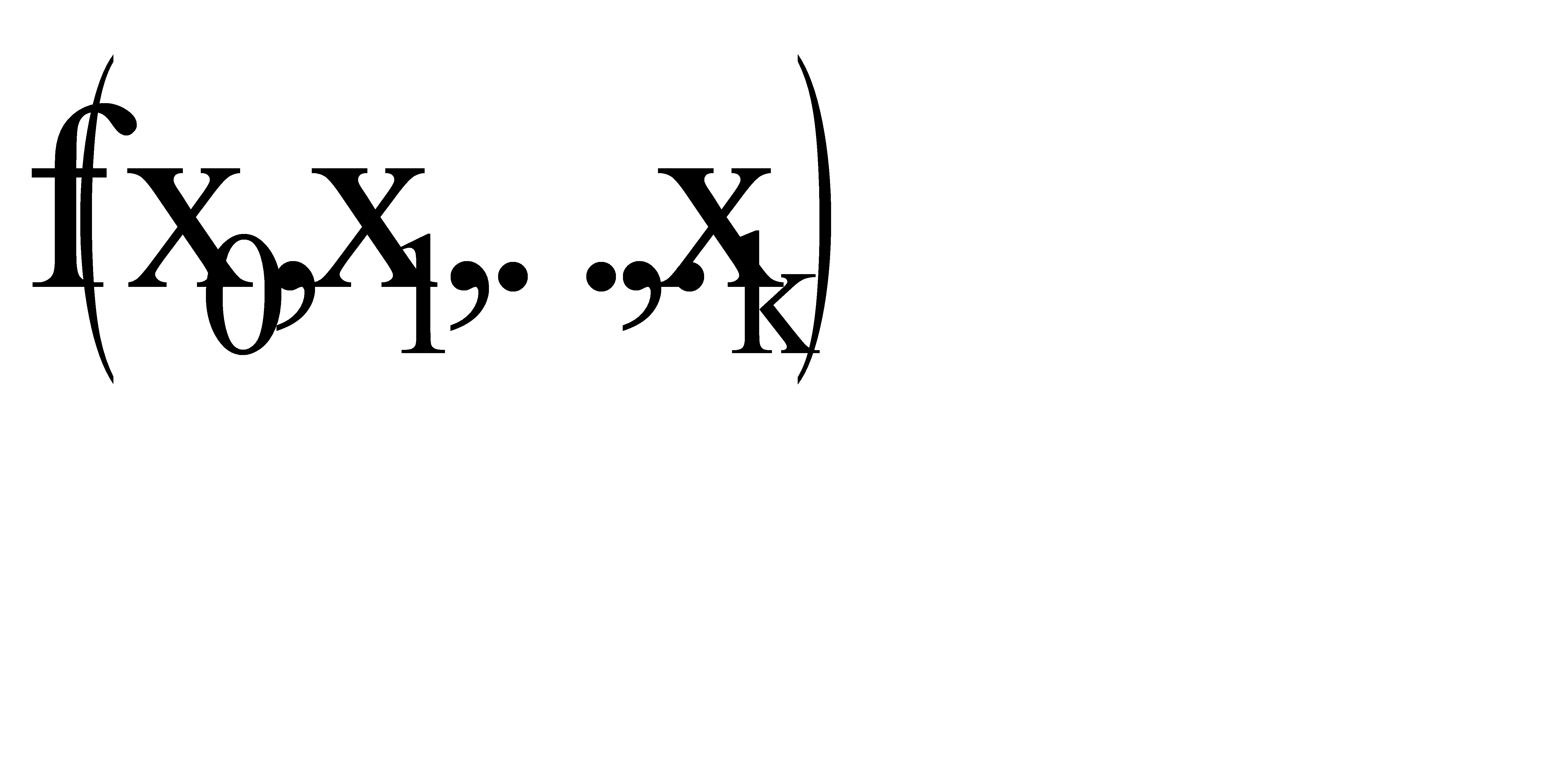 - есть разностное отношение k-го порядка.
- есть разностное отношение k-го порядка.
Учитывая выражение для В интерполяционный многочлен можно представить в виде
 .
.
Эта форма записи интерполяционного многочлена Лагранжа носит название интерполяционного многочлена Ньютона для неравных промежутков. Многочлен Ньютона имеет степень равную n и удовлетворяет условию
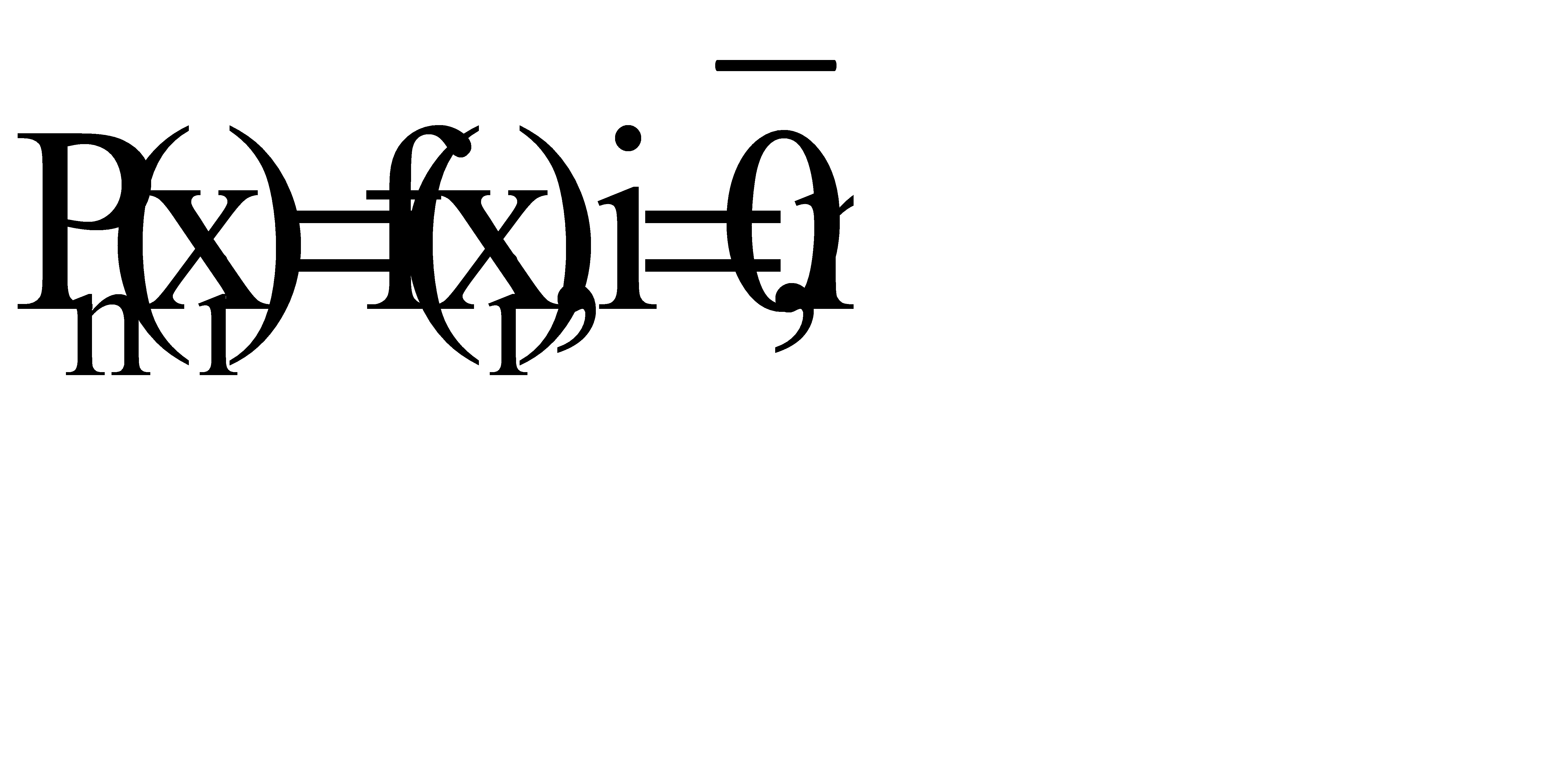 .
.
Формула Ньютона имеет более сложное строение, чем формула Лагранжа, и требует составления разностных отношений 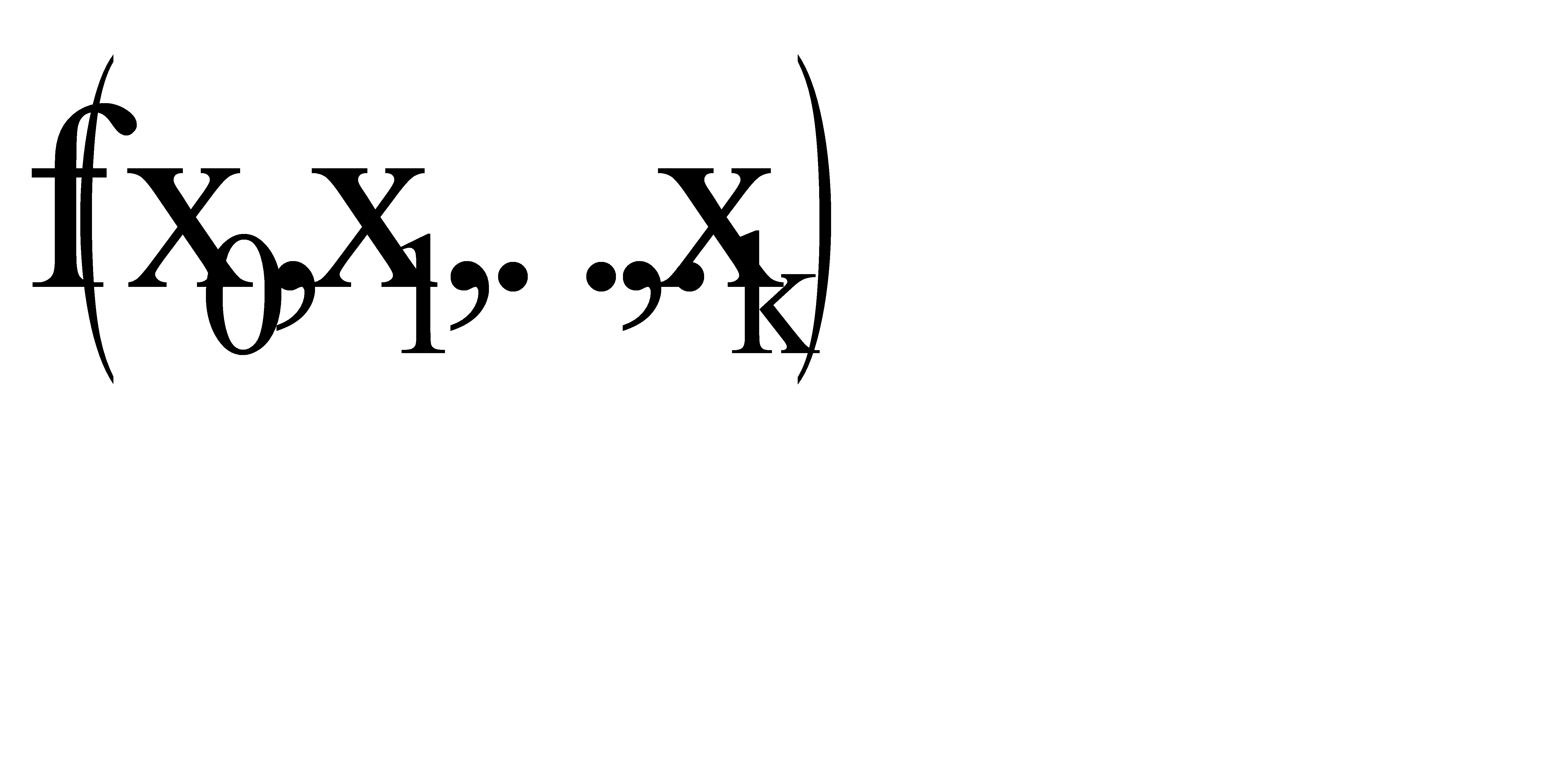 ,
, 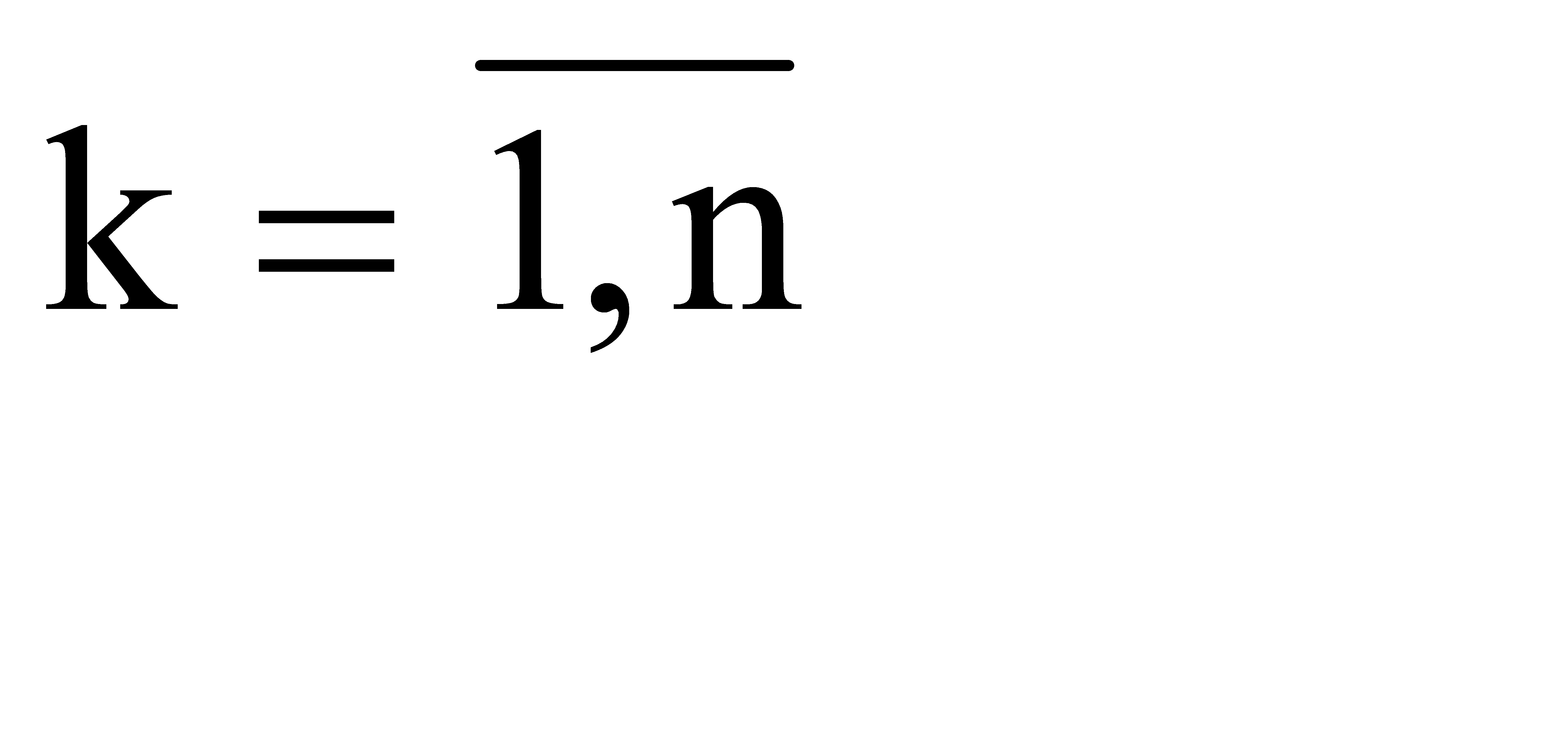 . Несмотря на это, она более удобна для вычислений, т.к. при добавлении нового узла все проделанные вычисления сохраняются, а в формуле добавляется еще одно слагаемое
. Несмотря на это, она более удобна для вычислений, т.к. при добавлении нового узла все проделанные вычисления сохраняются, а в формуле добавляется еще одно слагаемое  .
.
Это позволяет не задавать заранее число узлов интерполирования, а постепенно увеличивать точность результата, добавляя последовательно по одному новому узлу.
Остаточный член формулы Ньютона совпадает с остаточным членом формулы Лагранжа, т.е.
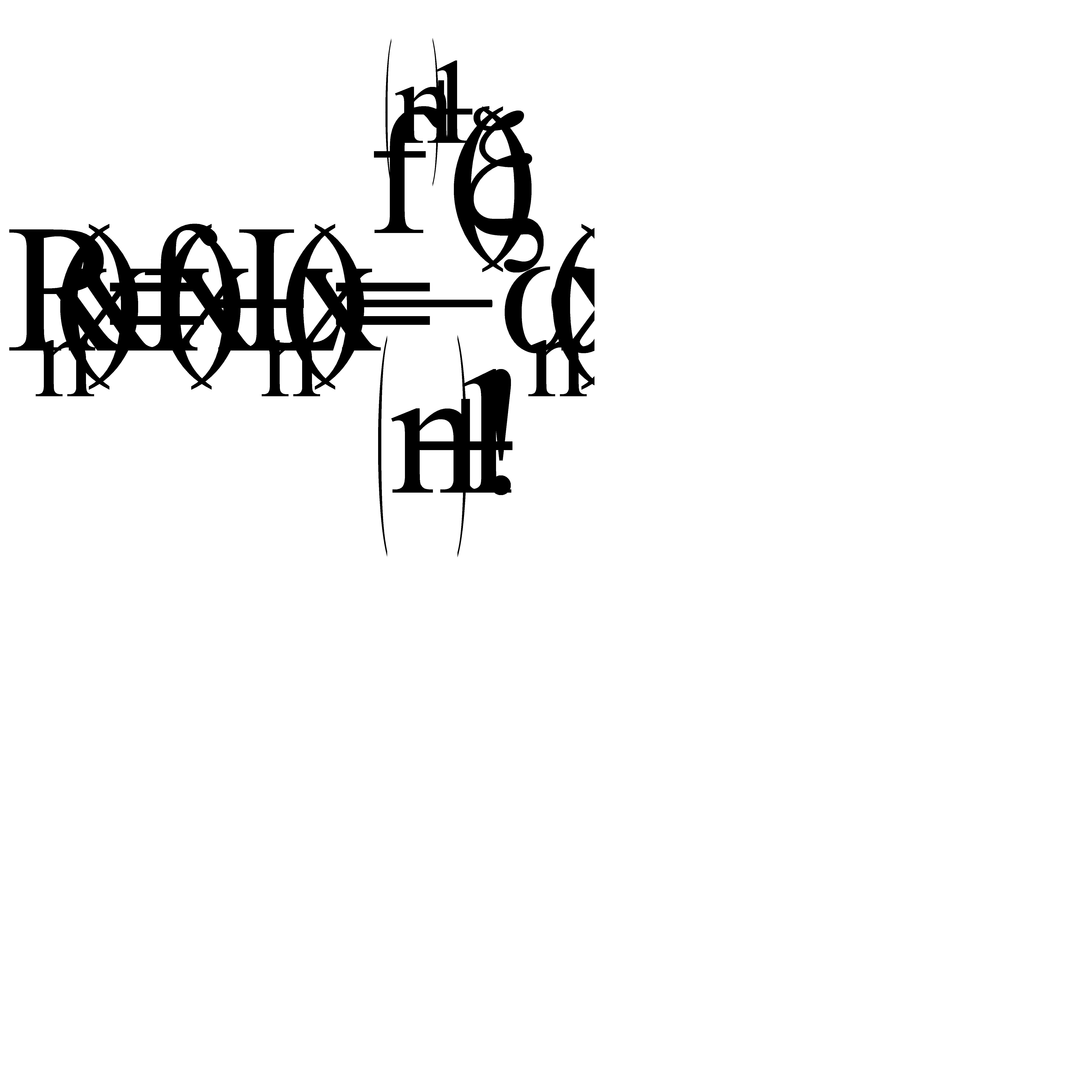
где x - точка отрезка, содержащего узлы интерполирования и точку х. Из свойств разностных отношений следует
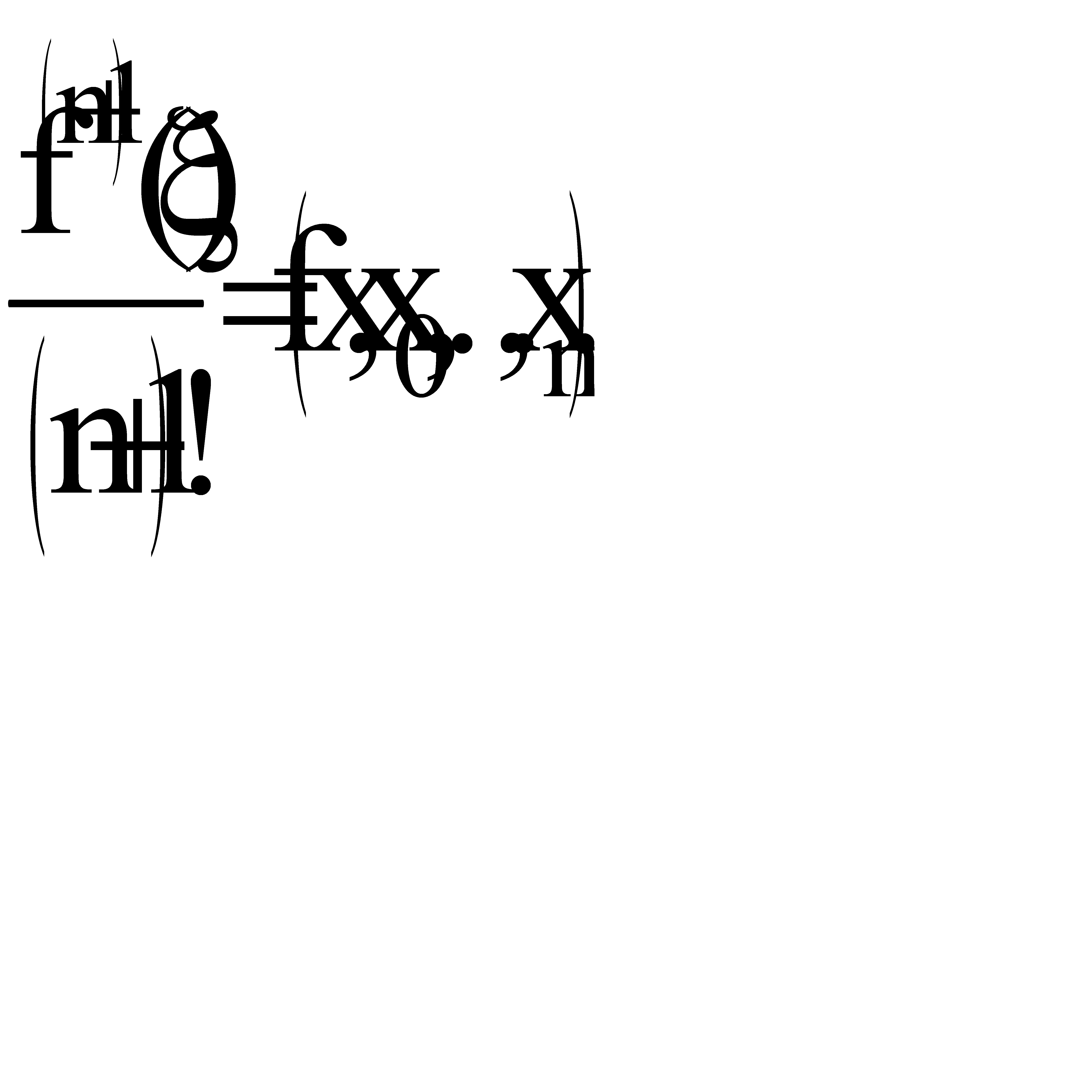 .
.
Тогда для остаточного члена имеем: 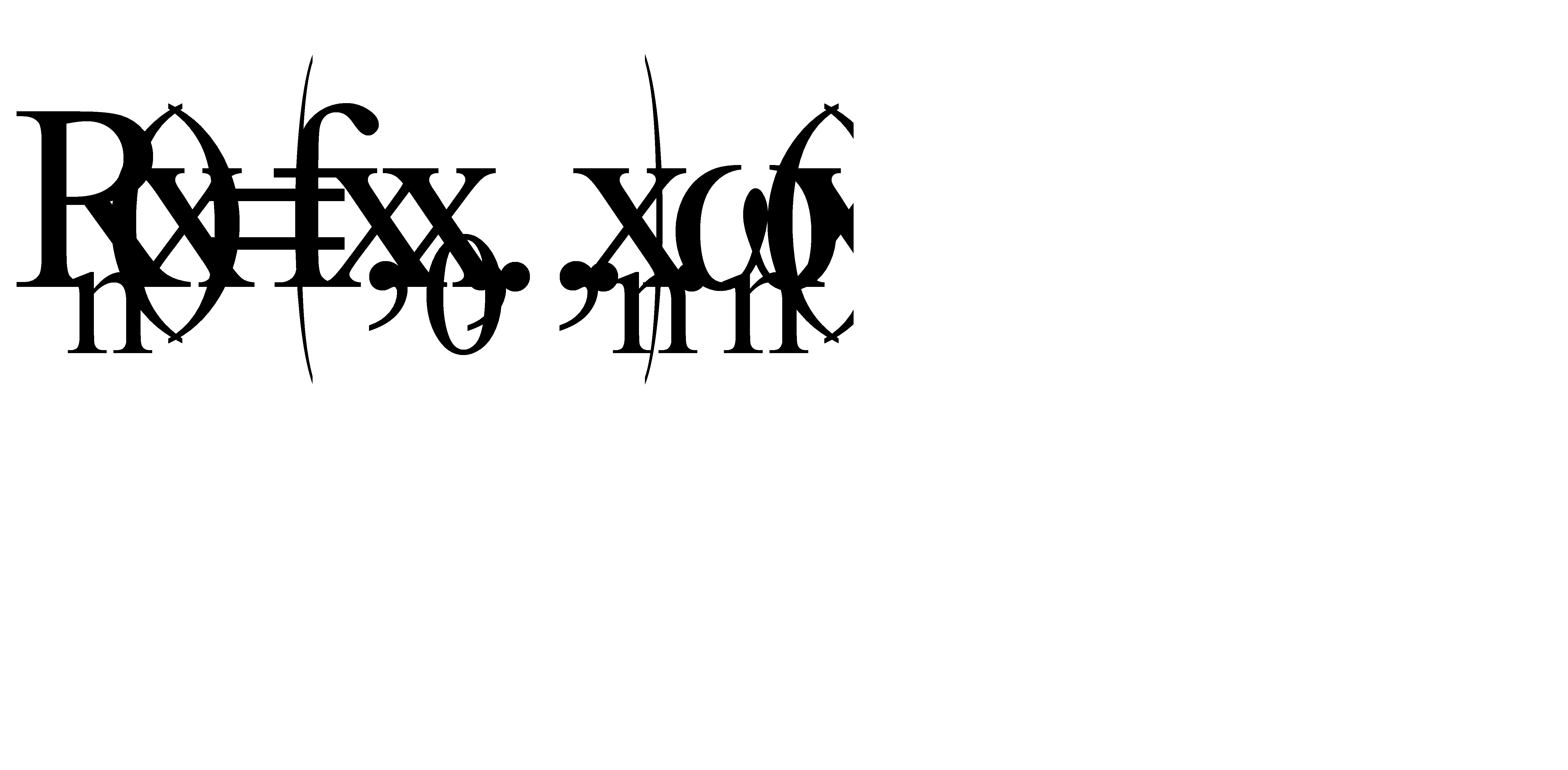 .
.
 2015-04-20
2015-04-20 519
519








