Метод Монте-Карло

Методы решения задач, использующие случайные величины, называются методами Монте-Карло.

Пусть методом Монте-Карло требуется вычислить m - кратный интеграл

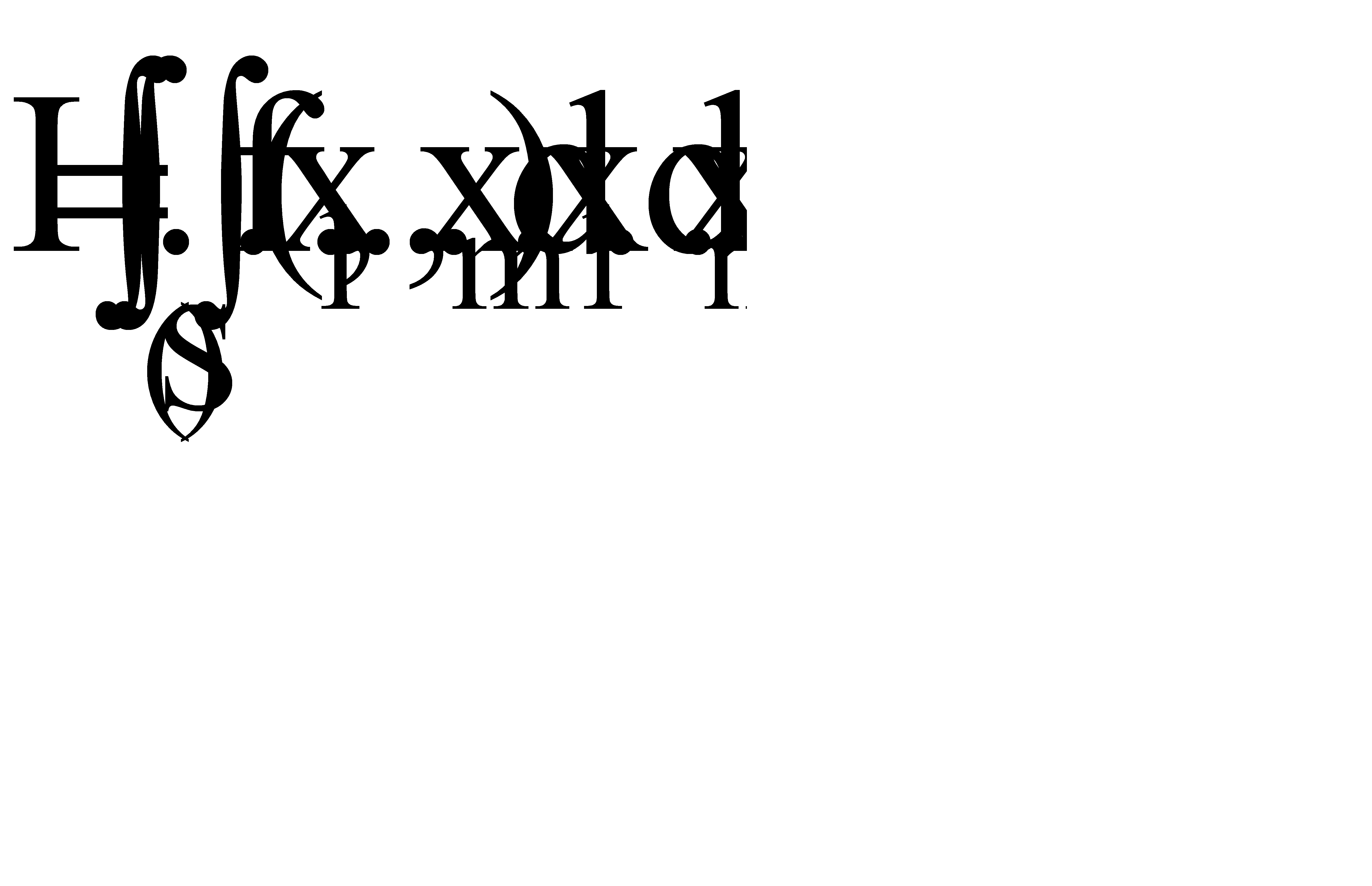, (17)

где функция f(x₁,...,x_m) задана в ограниченной замкнутой области S, а эта область заключена в m - мерном параллелепипеде . Для преобразования m - мерного параллелепипеда в m - мерный единичный куб сделаем замену переменных следующего вида: 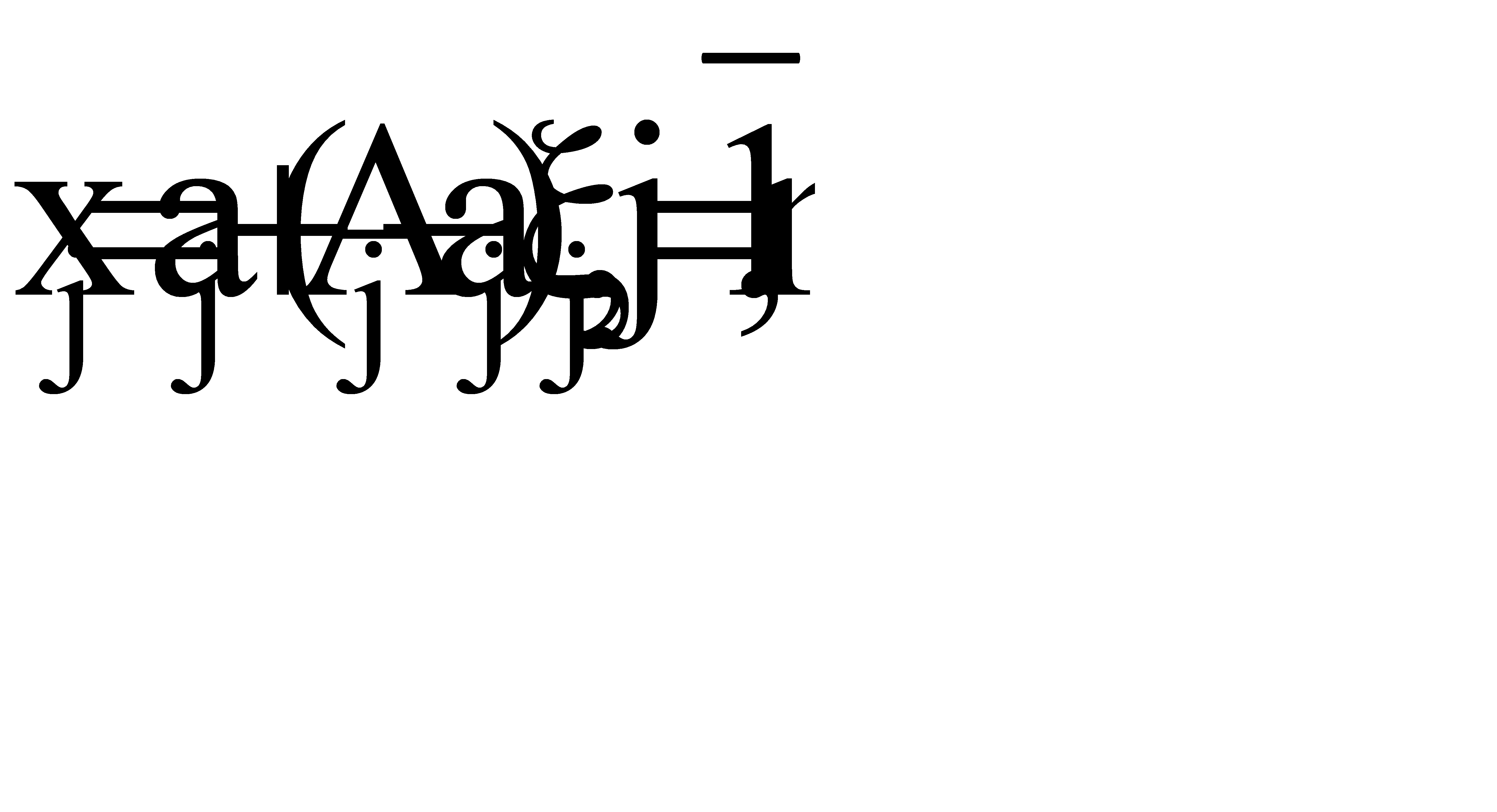, при этом 0£x_j£1. Якобиан этого преобразования

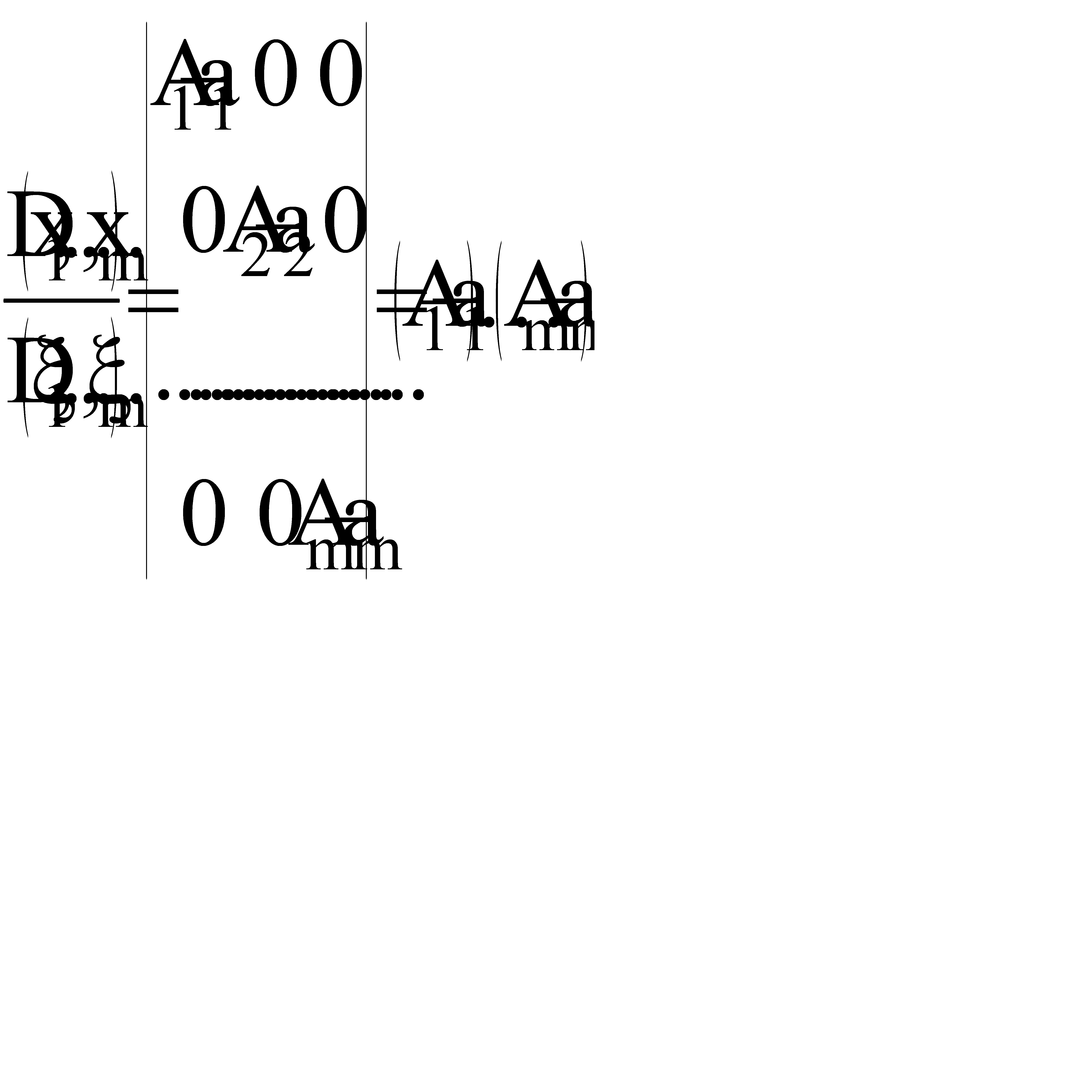
Тогда интеграл (17) перепишется в виде

, (18)

где , s - новая область интегрирования, лежащая внутри m - мерного единичного куба.

Выберем m равномерно распределенных на [0,1] последовательностей случайных чисел 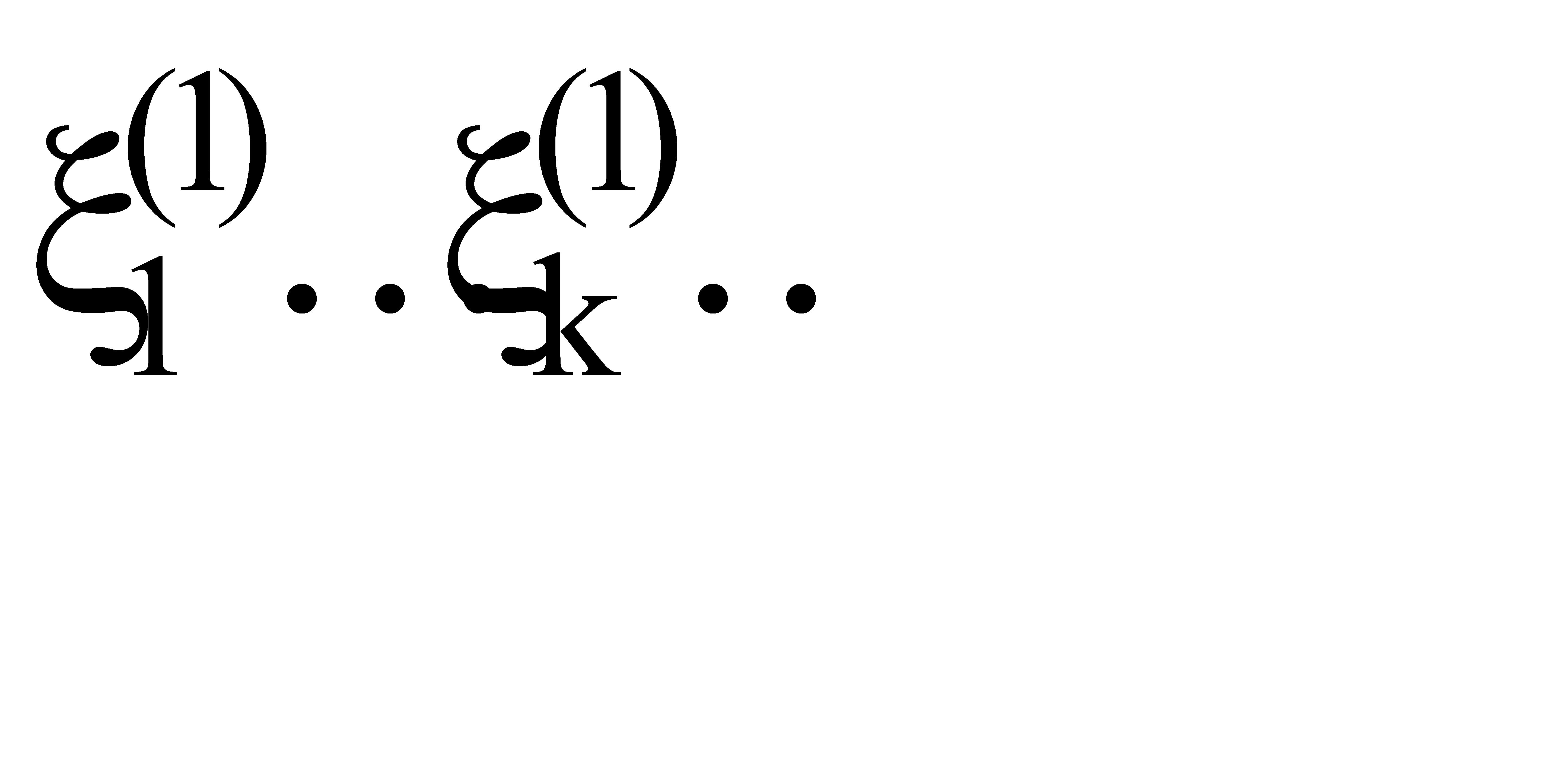; ¼, 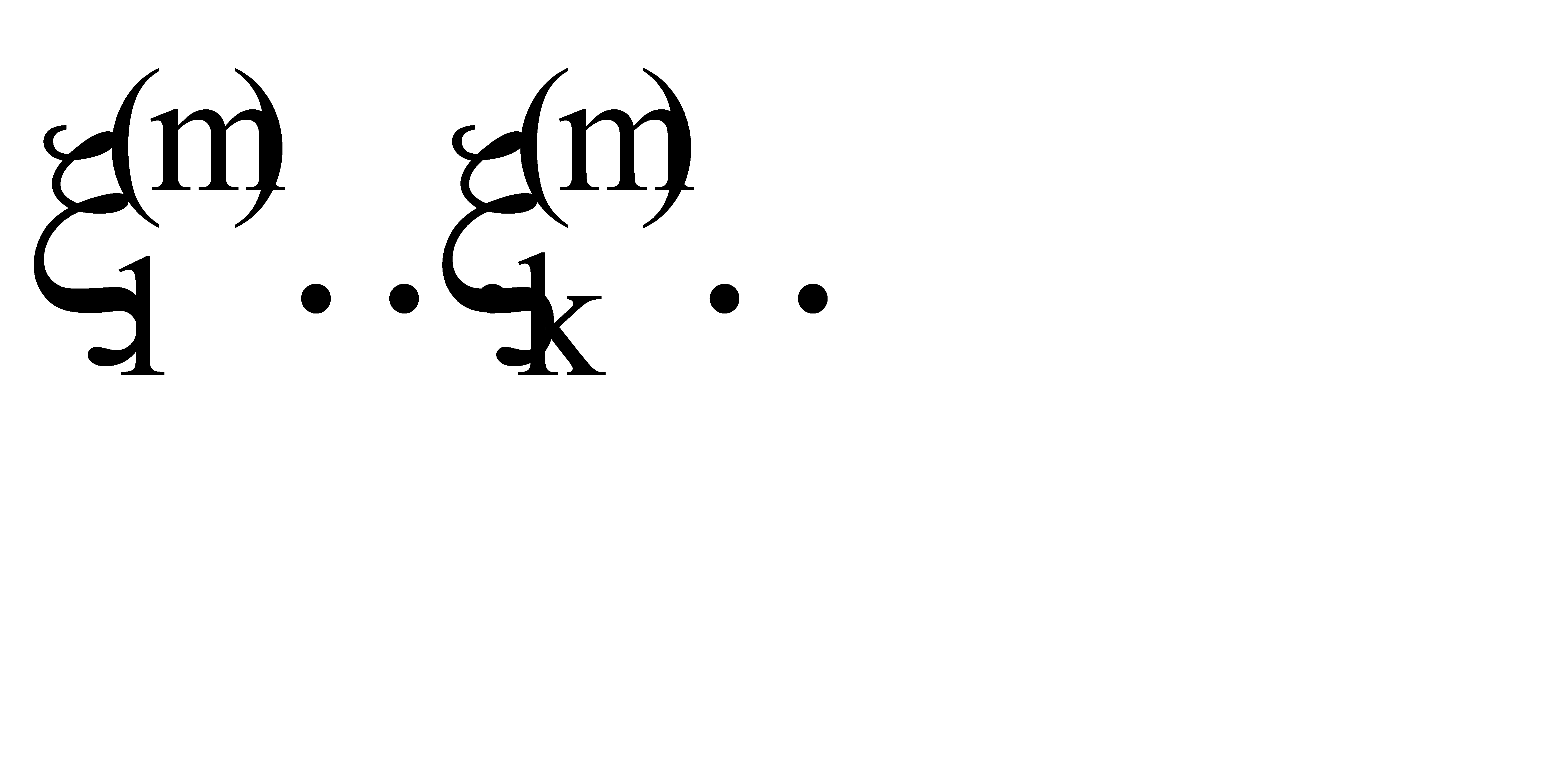. Точки можно рассматривать как случайные точки из m - мерного единичного куба. Будем считать, что n - случайных точек принадлежат области s, а (N-n) точек не принадлежат ей.

Если взять достаточно большое число n точек из области s, то приближенно можно считать

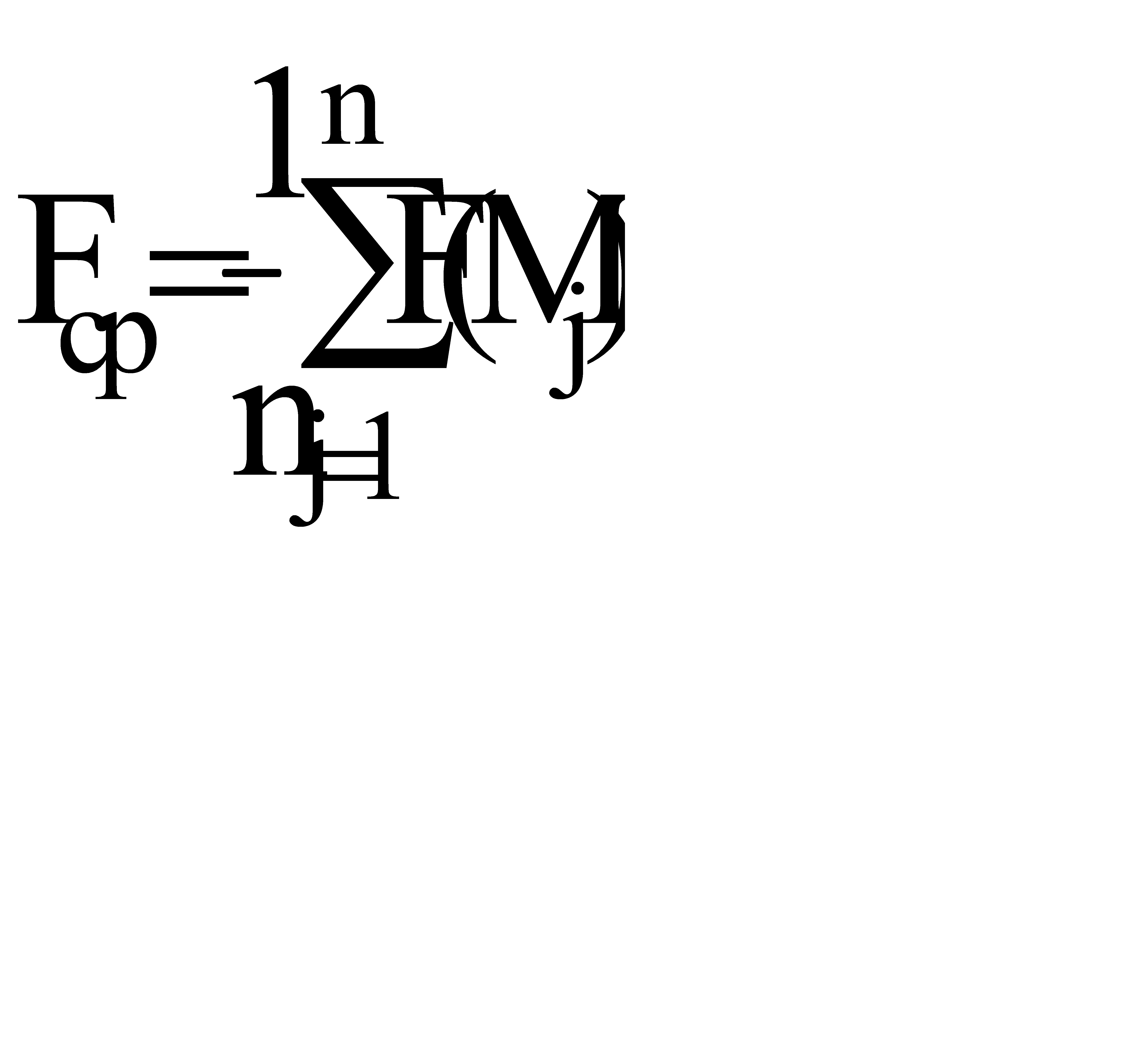, (19)

тогда выражение (18) можно переписать в виде

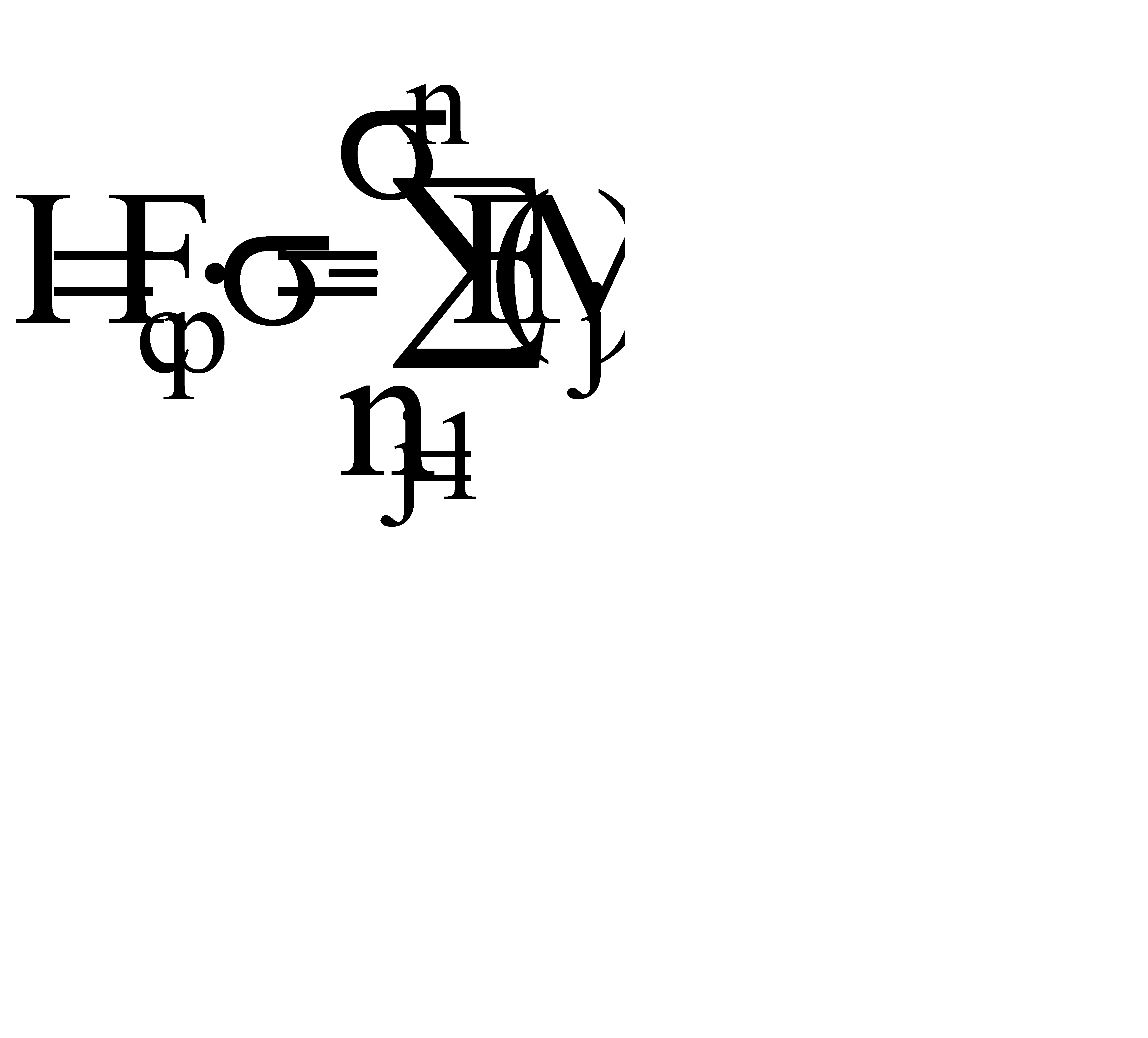, (20)

здесь s - объем области интегрирования. Если вычисление объема затруднительно, то можно считать, что 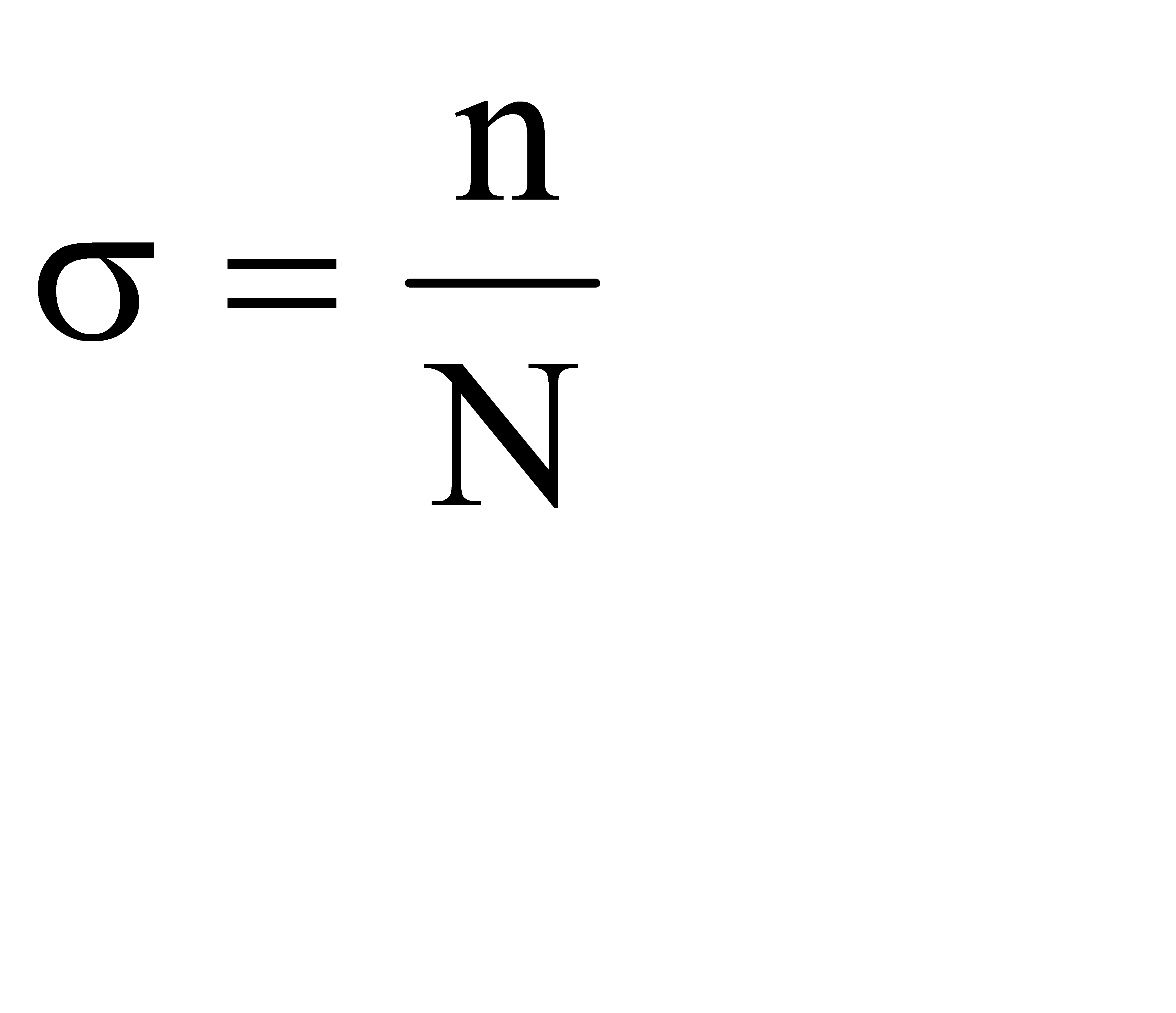, тогда

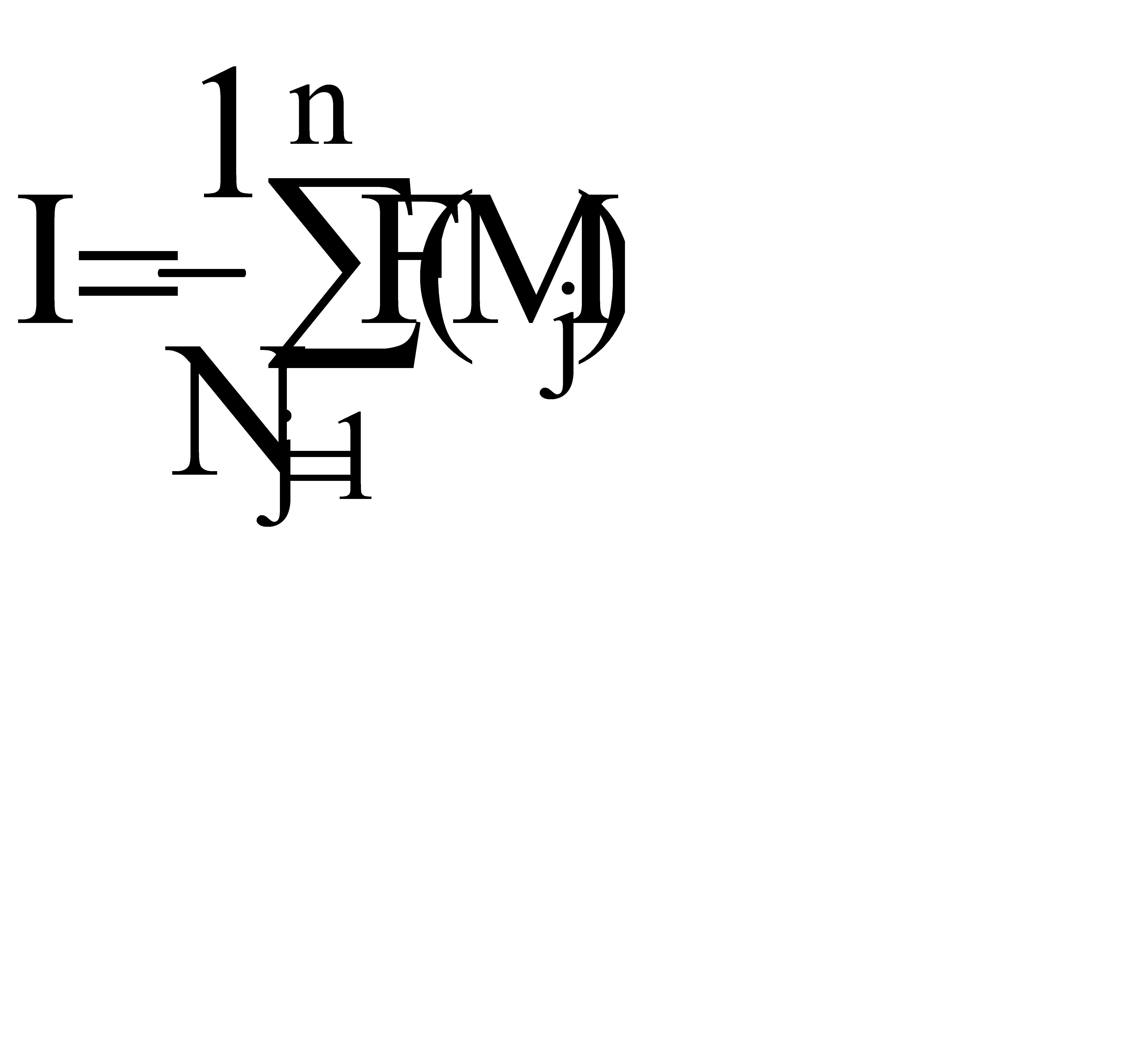. (21)