Отсутствие допустимых решений

Если ограничения задачи ЛП несовместны (т.е. они не могут выполняться одно-

временно), то задача не имеет допустимых решений. Такая ситуация не может воз-

никнуть, если все неравенства, составляющие систему ограничений, имеют тип "<"

с неотрицательными правыми частями, так как в этом случае дополнительные переменные могут составить допустимое решение. Для других типов ограничений используются искусственные переменные. И хотя в оптимальном решении все искусственные переменные в силу штрафов равны нулю, такой исход возможен только

тогда, когда задача имеет непустое пространство допустимых решений. В против-

ном случае в оптимальном решении будет присутствовать хотя бы одна положи-

тельная искусственная переменная.

С практической точки зрения отсутствие допустимых решений свидетельствует

о том, что задача плохо сформулирована.

9. Двойственная задача. Определение.

При изложении теории двойственности часто рассматривают формулировки двойственной задачи в зависимости от различных видов прямой задачи, которые определяются типами ограничений, знаками переменных (неотрицательные или свободные, т.е. без ограничения в знаке) и типом оптимизации (максимизация или минимизация целевой функции). Приведем единую формулировку двойственной задачи, применимую ко всем видам прямой задачи. В основу такой формулировки положена стандартная форма прямой задачи. Напомним, что задача ЛП в стандартной форме записывается следующим образом. Максимизировать или минимизировать целевую функцию

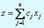
при ограничениях

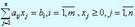
В состав n переменных хj входят также дополнительные переменные. Стандартная форма задачи линейного программирования предполагает выполнение следующих условий.

Все ограничения записаны в виде равенств (с неотрицательной правой частью).

Все переменные неотрицательны.

Оптимизация определяется как максимизация или минимизация целевой функции.

Стандартная форма задачи линейного программирования порождает стандартную таблицу симплекс-метода. Решение двойственной задачи можно получить непосредственно из симплекс-таблицы, соответствующей оптимальному решению прямой задачи. Таким образом, определив двойственную задачу на основе стандартной формы прямой задачи, после вычислений симплекс-метода мы автоматически получаем решение двойственной задачи. Переменные и ограничения двойственной задачи формируются путем симметричных структурных преобразований прямой задачи по следующим правилам:

Каждому из m ограничений прямой задачи соответствует переменная двойственной задачи.

Каждой из n переменных прямой задачи соответствует ограничение двойственной задачи.

Коэффициенты при какой-либо переменной в ограничениях прямой задачи становятся коэффициентами ограничения двойственной задачи, соответствующей этой переменной, а правая часть формируемого ограничения равна коэффициенту при этой переменной в выражении целевой функции.

Коэффициенты целевой функции двойственной задачи равны правым частям ограничений прямой задачи.

10. Соотношение между прямой и двойственными задачами.

Изменение коэффициентов целевой функции и ограничений задачи ЛП влияет

на оптимальность и допустимость текущего оптимального решения. Поэтому необходимо выяснить, как вычисления в симплекс-методе зависят от изменений

коэффициентов исходной задачи. В частности, следует выяснить, как от этих изменений зависят оптимальность и допустимость решения, представленного в ви-

де симплекс-таблицы.

Наиболее компактный способ записи вычислений, производимых при симплекс-

методе, заключается в использовании матриц. Для этого в начале данного раздела

приведем краткий обзор действий над матрицами, а затем рассмотрим соотношение

между оптимальными решениями прямой и двойственной задач.

11. Экономическая интерпретация двойственности.

12. Анализ чувствительности оптимального решения.

13. Алгоритм решения транспортной задачи.

Последовательность этапов алгоритма решения транспортной задачи в точности

повторяет аналогичную последовательность этапов симплексного алгоритма.

Шаг 1. Определяем начальное базисное допустимое решение, затем пере-

ходим к выполнению второго этапа.

Шаг 2. На основании условия оптимальности симплекс-метода среди

всех небазисных переменных определяем вводимую в базис. Если

все небазисные переменные удовлетворяют условию оптимальности, вычисления заканчиваются; в противном случае переходим к третьему этапу.

Шаг 3. С помощью условия допустимости симплекс-метода среди текущих базисных переменных определяем исключаемую. Затем находим новое базисное решение. Возвращаемся ко второму этапу.

Рассмотрим каждый описанный этап в отдельности.

Определение начального решения

Общая транспортная модель с т пунктами отправления и п пунктами назначения имеет т + п ограничений в виде равенств, по одному на каждый пункт отправления и назначения. Поскольку транспортная модель всегда сбалансирована

(сумма предложений равна сумме спроса), одно из этих равенств должно быть избыточным. Таким образом, транспортная модель имеет т + п - 1 независимых ограничений, отсюда следует, что начальное базисное решение состоит из т + п - 1

базисных переменных. Например, начальное решение в примере 5.3.1 содержит

3 + 4-1=6 базисных переменных.

Специальная структура транспортной модели для построения начального решения позволяет применить следующие методы (вместо использования искусственных переменных, как это делается в симплекс-методе).

1. Метод северо-западного угла.

2. Метод наименьшей стоимости.

3. Метод Фогеля.

Различие этих методов заключается в "качестве" начального решения, т.е.

"удаленности" начального решения от оптимального. В общем случае метод Фогеля дает наилучшее решение, а метод северо-западного угла — наихудшее. Однако

метод северо-западного угла требует меньшего объема вычислений.

Метод северо-западного угла. Выполнение начинается с верхней левой ячейки

(северо-западного угла) транспортной таблицы, т.е. с переменной хп.

Шаг 1. Переменной хп присваивается максимальное значение, допускаемое ограничениями на спрос и предложение.

Шаг 2. Вычеркивается строка (или столбец) с полностью реализованным

предложением (с удовлетворенным спросом). Это означает, что

в вычеркнутой строке (столбце) мы не будем присваивать значения

остальным неременным (кроме переменной, определенной на первом этапе). Если одновременно удовлетворяются спрос и предложение, вычеркивается только строка или только столбец.

Шаг 3. Если не вычеркнута только одна строка или только один столбец,

процесс останавливается. В противном случае переходим к ячейке

справа, если вычеркнут столбец, или к нижележащей ячейке,

14. Интерпретация метода потенциалов как симплекс-метода.

Связь метода потенциалов с симплекс-методом основывается на соотношениях

двойственности задач ЛП (раздел 4.2). Исходя из специальной структуры транс-

портной задачи (обратитесь к примеру 5.5.1, где показано, как транспортную

задачу представить в виде стандартной задачи ЛП), двойственная ей задача будет

записана в следующем виде.

Максимизировать z = 2]а,и(+ У^б.у,

i=i;=1

при ограничениях

и. + и. < сц для всех I и у,

ulnvj — свободные переменные,

где

~а1 — предложение (объем грузов) пункта отправления i,

bt — спрос (заявка на грузы) пункта назначения/,

ctj — стоимость перевозки единицы груза из пункта отправления i в пункт

назначения/,

ц, — двойственная переменная, соответствующая ограничению на предложение пункта отправления i,

iv — двойственная переменная, соответствующая ограничению на спрос

пункта назначения/.

Из формулы 2 раздела 4.2.4 следует, что коэффициент при переменной хц

в выражении целевой функции должен быть равен разности между левой

и правой частями соответствующего ограничения двойственной задачи, т.е. ве-

личине u(+ v/ - сц. Но как мы уже знаем, эта величина должна быть равной нулю

для каждой базисной переменной. Другими словами, для этих переменных

должно выполняться равенство ut + v} = сц. Имея т + п - 1 таких равенств и ре шая их как систему линейных уравнений (после присвоения какой-либо переменной

произвольного значения, например и, = 0), находим значения потенциалов их и иу.

Вычислив значения потенциалов, далее определяем вводимую в базис переменную среди всех небазисных как переменную, имеющую наибольшее положительное значение величины u, + v: - сц.

Присвоение одной из двойственных переменных произвольного значения

(например, и1 = 0) противоречит представлениям раздела 4.2.3, поскольку это

присвоение показывает, что, возможно, решение двойственной задачи (определяется

вычисленными значениями двойственных переменных (потенциалов)) не единственное. В действительности противоречия здесь нет, и решение упражнения 5.3.3.2 объясняет, — почему.

15. Сетевые модели. Основные понятия.

В рамках теории исследования операций рассматривается большое количество

практических задач, которые можно сформулировать и решить как сетевые моде-

ли. Недавние исследования показывают, что не менее 70% реальных задач математического программирования можно представить в виде сетевых моделей. Приведем несколько конкретных примеров.

1. Проектирование газопровода, соединяющего буровые скважины морского

базирования с находящейся на берегу приемной станцией. Целевая функция

соответствующей модели должна минимизировать стоимость строительства

газопровода.

2. Поиск кратчайшего маршрута между двумя городами по существующей

сети дорог.

3. Определение максимальной пропускной способности трубопровода для

транспортировки угольной пульпы от угольных шахт к электростанциям.

Сеть состоит из множества узлов, связанных дугами (или ребрами).1 Таким

образом, сеть описывается парой множеств (N, А), где N— множество узлов,

а А— множество ребер. Например, сеть, показанная на рис. 6.1, описывается

следующим образом.

N={1,2,3,4,5},

А = {A, 2), A, 3), B, 3), B, 5), C, 4), C, 5), D, 2), D, 5)}.

С каждым типом сети связан определенный тип потоков (например, транспортный поток нефти в нефтепроводах или автомобильные потоки в сети городских до-

рог). В общем случае потоки в сети ограничены пропускной способностью ее ребер,

которая может быть как конечной, так и бесконечной.

Ребро называется направленным, или ориентированным (и в этом случае ребро

будем называть дугой), если в одном направлении возможен только положительный поток, а в противоположном — только нулевой. В ориентированной сети все

ребра ориентированы.

Путем называется последовательность различных ребер, соединяющих два уз-

ла, независимо от направления потока в каждом ребре. Путь формирует цикл, если

начальный и конечный узлы совпадают. Например, на рис. 6.1 дуги B, 3), C, 4)

и D, 2) составляют цикл. Ориентированный цикл — это цикл, в котором все дуги

ориентированы в определенном направлении.

Связная сеть — такая сеть, у которой любые два узла связаны по крайней мере

одним путем. На рис. 6.1 показан именно такой тип сети. Деревом называется

связная сеть, содержащая подмножество узлов исходной сети и не имеющая циклов. Остовное дерево'— это дерево, содержащее все узлы сети.

16. Алгоритм построения минимального остовного дерева.

Алгоритм построения минимального остовного дерева предполагает соединение

всех узлов сети с помощью путей наименьшей длины. Типичной задачей, для решения которой необходим такой алгоритм, является создание (проектирование) сети

дорог с твердым покрытием, соединяющих населенные пункты в сельской местности,

где дороги, соединяющие два каких-либо пункта, могут проходить через другие населенные пункты. Наиболее экономичный проект дорожной системы должен минимизировать общую длину дорог с твердым покрытием, при этом желаемый результат

можно получить с помощью алгоритма построения минимального остовного дерева.

Опишем процедуру выполнения этого алгоритма. Обозначим через N = {1, 2,..., п)

множество узлов сети и введем новые обозначения:

С4 — множество узлов сети, соединенных алгоритмом после выполнения k-й

итерации этого алгоритма,

Ск — множество узлов сети, не соединенных с узлами множества Ch после выполнения k-й итерации этого алгоритма.

Этап 0. Пусть Со = 0 и Со = N.

Этап 1. Выбираем любой узел i из множества Со и определяем С, = {i}, тогда С, = N - {i}. Полагаем k — 2.

Основной этап к. В множестве Ск_, выбираем узел/, который соединен самой

короткой дугой с каким-либо узлом из множества Ct_,. Узел / при-

соединяется к множеству С^ и удаляется из множества Ct_,. Та-

ким образом, С, = Ск_, + {/}, Ct = Ct_, - {/}.

Если множество Ск пусто, то выполнение алгоритма заканчивается.

В противном случае полагаем k — k + 1 и повторяем последний этап.

17. Алгоритм Дейкстры.

В процессе выполнения этого алгоритма при переходе от

узла i к следующему узлу / используется специальная процедура пометки ребер.

Обозначим через и, кратчайшее расстояние от исходного узла 1 до узла i, через dtj —

длину ребра (г, j). Тогда для узла у определим метку [uJt i] следующим образом.

[uj,i] = [ul + dli,i],dli>0

Метки узлов в алгоритме Дейкстры могут быть двух типов: временные и постоянные. Временная метка впоследствии может быть заменена на другую временную,

если будет найден более короткий путь к данному узлу. Когда же станет очевидным, что не существует более короткого пути от исходного узла к данному, статус

временной метки изменяется на постоянный.

Вычислительная схема алгоритма состоит из следующих этапов.

Этап 0. Исходному узлу (узел 1) присваивается постоянная метка [0, —].

Полагаем i = 1.

Этап 1.

а) Вычисляются временные метки [и: + dtj, t] для всех узлов у, которые можно

достичь непосредственно из узла i и которые не имеют постоянных ме-

Глава 6. Сетевые модели

ток. Если узел j уже имеет метку [uy, k], полученную от другого узла k, и,

если и, + dtj < ujt тогда метка [и., k] заменяется на [u, + dljt i].

b) Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном случае выбирается метка [ur, s] с наименьшим значением расстояния иг среди всех временных меток (если таких меток несколько, то выбор произволен). Полагаем i = г и повторяем этап i.

18. Алгоритм Флойда.

Этот алгоритм более общий по сравнению с алгоритмом

Дейкстры, так как он находит кратчайшие пути между любыми двумя узлами

сети. В этом алгоритме сеть представлена в виде квадратной матрицы с п строками и п столбцами. Элемент (?, у) равен расстоянию dtj от узла i к узлу j, кото-

рое имеет конечное значение, если существует дуга (i, j), и равен бесконечности

в противном случае.

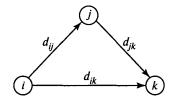
Покажем сначала основную идею метода Флойда. Пусть есть три узла i, j и k

и заданы расстояния между ними (рис. 6.19). Если выполняется неравенство

dll + djh<dtk, то целесообразно заменить путь i->fe путем i->j->k. Такая замена

(далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.

Алгоритм Флойда требует выполнения следующих действий.

Этап 0. Определяем начальную матрицу расстояний Do и матрицу последовательности узлов So. Диагональные элементы обеих матриц

помечаются знаком "—", показывающим, что эти элементы в вычислениях не участвуют. Полагаем к = 1.

Основной этап к. Задаем строку k и столбец k как ведущую строку и ведущий

столбец. Рассматриваем возможность применения треугольного

оператора ко всем элементам dtj матрицы Dk^. Если выполняется

неравенство

dtk + dkj < dtj, (i*k,j*kui*j),

то делаем следующее:

a) создаем матрицу Dk путем замены в матрице Dk_1 элемента dl}

суммой dlk + dhj,

b) создаем матрицу Sk, меняя в матрице S4_j элемент st/ на k. Пола-

гаем k — k + lu повторяем этап k.

Поясним действия, выполняемые на k-м этапе алгоритма, представив матрицу

Dk_l так, как она показана на рис. 6.20. На этом рисунке строка k и столбец k являются ведущими. Строка i — любая строка с номером от 1 до k - 1, а строка р —

произвольная строка с номером от k + 1 до п. Аналогично столбец j представляет

любой столбец с номером от 1 до k - 1, а столбец q — произвольный столбец с номе-

ром от k + 1 до п. Треугольный оператор выполняется следующим образом. Если

сумма элементов ведущих строки и столбца (показанных в квадратиках) меньше

элементов, находящихся на пересечении столбца и строки (показаны в кружках),

соответствующих рассматриваемым ведущим элементам, то расстояние (элемент

в кружке) заменяется суммой расстояний, представленных ведущими элементами.

После реализации п этапов алгоритма определение по матрицам Dn и Sn кратчайшего пути между узлами i и j выполняется по следующим правилам.

1. Расстояние между узлами i и у равно элементу dtj в матрице Dn.

2. Промежуточные узлы пути от узла i к узлу j определяем по матрице Sn.

Пусть s0 = k, тогда имеем путь i -» k -» j. Если далее slk = k и shi = j, тогда

считаем, что весь путь определен, так как найдены все промежуточные узлы. В противном случае повторяем описанную процедуру для путей от узла

i к узлу k и от узла k к узлу у.

19. Целочисленное программирование.

Целочисленное линейное программирование (ЦЛП) ориентировано на решение

задач линейного программирования, в которых все или некоторые переменные

должны принимать целочисленные (или дискретные) значения. Несмотря на интенсивные исследования, проводимые на протяжении последних десятилетий, известные вычислительные методы решения задач ЦЛП далеки от совершенства. На

сегодня не существует надежных вычислительных алгоритмов решения таких задач.