Общее уравнение прямой.
Другими словами, уравнение прямой на плоскости в прямоугольной системе координат Oxy есть некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой.
Общее уравнение прямой. Уравнение 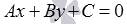 называется общим уравнением прямой на плоскости (задает прямую линию в прямоугольной системе координат Oxy на плоскости).
называется общим уравнением прямой на плоскости (задает прямую линию в прямоугольной системе координат Oxy на плоскости). 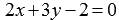
Уравнение прямой в отрезках.
Уравнение прямой вида 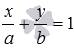 , где a и b – некоторые действительные числа отличные от нуля, называется уравнением прямой в отрезках. Это название не случайно, так как абсолютные величины чисел а и b равны длинам отрезков, которые прямая отсекает на координатных осях Ox и Oy соответственно (отрезки отсчитываются от начала координат). Таким образом, уравнение прямой в отрезках позволяет легко строить эту прямую на чертеже. Для этого следует отметить в прямоугольной системе координат на плоскости точки с координатами
, где a и b – некоторые действительные числа отличные от нуля, называется уравнением прямой в отрезках. Это название не случайно, так как абсолютные величины чисел а и b равны длинам отрезков, которые прямая отсекает на координатных осях Ox и Oy соответственно (отрезки отсчитываются от начала координат). Таким образом, уравнение прямой в отрезках позволяет легко строить эту прямую на чертеже. Для этого следует отметить в прямоугольной системе координат на плоскости точки с координатами 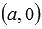 и
и 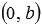 , и с помощью линейки соединить их прямой линией.
, и с помощью линейки соединить их прямой линией.
Уравнение прямой с угловым коэффициентом.
Уравнение прямой вида 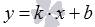 , где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент). Уравнения прямой с угловым коэффициентом нам хорошо известны из курса алгебры средней школы. Такой вид уравнения прямой очень удобен для исследования, так как переменная y представляет собой явную функцию аргумента x. K=tga
, где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент). Уравнения прямой с угловым коэффициентом нам хорошо известны из курса алгебры средней школы. Такой вид уравнения прямой очень удобен для исследования, так как переменная y представляет собой явную функцию аргумента x. K=tga
Каноническое уравнение прямой на плоскости.
Каноническое уравнение прямой на плоскости в прямоугольной декартовой системе координат Oxy имеет вид 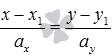 , где
, где 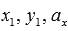 и
и 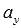 – некоторые действительные числа, причем и одновременно не равны нулю.
– некоторые действительные числа, причем и одновременно не равны нулю.
Очевидно, что прямая линия, определяемая каноническим уравнением прямой, проходит через точку 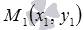 . В свою очередь числа
. В свою очередь числа 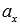 и
и 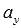 , стоящие в знаменателях дробей, представляют собой координаты направляющего вектора этой прямой. Таким образом, каноническое уравнение прямой
, стоящие в знаменателях дробей, представляют собой координаты направляющего вектора этой прямой. Таким образом, каноническое уравнение прямой 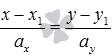 в прямоугольной системе координат Oxy на плоскости соответствует прямой, проходящей через точку
в прямоугольной системе координат Oxy на плоскости соответствует прямой, проходящей через точку 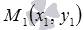 и имеющей направляющий вектор
и имеющей направляющий вектор 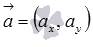 .
.
Для примера изобразим на плоскости прямую линию, соответствующую каноническому уравнению прямой вида 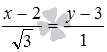 . Очевидно, что точка
. Очевидно, что точка  принадлежит прямой, а вектор является направляющим вектором
принадлежит прямой, а вектор является направляющим вектором 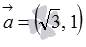 этой прямой.
этой прямой.
Параметрические уравнения прямой на плоскости.
Параметрические уравнения прямой на плоскости имеют вид 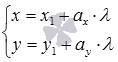 , где
, где 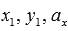 и
и 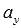 – некоторые действительные числа, причем
– некоторые действительные числа, причем 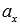 и
и 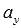 одновременно не равны нулю, а
одновременно не равны нулю, а 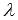 - параметр, принимающий любые действительные значения.
- параметр, принимающий любые действительные значения.
Параметрические уравнения прямой устанавливают неявную зависимость между абсциссами и ординатами точек прямой линии с помощью параметра 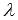 (отсюда и название этого вида уравнений прямой).
(отсюда и название этого вида уравнений прямой).
Пара чисел 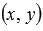 , которые вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра
, которые вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра 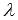 , представляет собой координаты некоторой точки прямой. К примеру, при
, представляет собой координаты некоторой точки прямой. К примеру, при 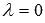 имеем
имеем 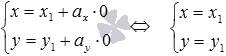 , то есть, точка с координатами
, то есть, точка с координатами 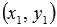 лежит на прямой.
лежит на прямой.
Следует отметить, что коэффициенты 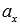 и
и 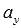 при параметре
при параметре 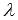 в параметрических уравнениях прямой являются координатами направляющего вектора этой прямой.
в параметрических уравнениях прямой являются координатами направляющего вектора этой прямой.
Для примера приведем параметрические уравнения прямой вида 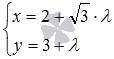 . Эта прямая в прямоугольной системе координат Oxy на плоскости проходит через точку с координатами
. Эта прямая в прямоугольной системе координат Oxy на плоскости проходит через точку с координатами 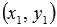 и имеет направляющий вектор
и имеет направляющий вектор 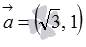
Нормальное уравнение прямой.
Если в общем уравнении прямой вида 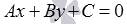 числа А, В и С таковы, что длина вектора
числа А, В и С таковы, что длина вектора 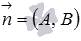 равна единице, а
равна единице, а 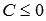 , то это общее уравнение прямой называется нормальным уравнением прямой. Нормальное уравнение прямой определяет в прямоугольной системе координат Oxy прямую линию, нормальным вектором которой является вектор
, то это общее уравнение прямой называется нормальным уравнением прямой. Нормальное уравнение прямой определяет в прямоугольной системе координат Oxy прямую линию, нормальным вектором которой является вектор 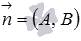 , причем эта прямая проходит на расстоянии
, причем эта прямая проходит на расстоянии 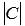 от начала координат в направлении вектора
от начала координат в направлении вектора 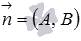 .
.
 2015-04-30
2015-04-30 8016
8016
