Плоскости в пространстве (типы уравнений)

13.) Прямая в пространстве

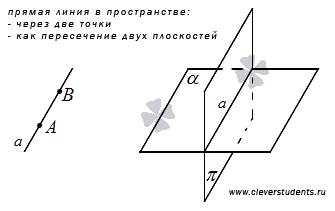
Взаимное расположение прямых в пространстве.

Перейдем к вариантам взаимного расположения двух прямых в пространстве.

Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).

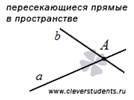
Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. В этом случае эти две прямые лежат в некоторой плоскости трехмерного пространства. Если две прямые в пространстве пересекаются, то мы приходим к понятию угла между пересекающимися прямыми.

В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек. Рекомендуем к изучению статью параллельные прямые, параллельность прямых.

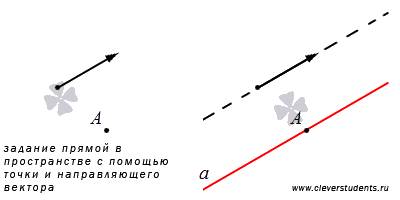
Любой ненулевой вектор, лежащий на прямой или ей параллельной прямой-направляющий вектор.

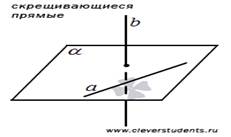
Наконец, две прямые в трехмерном пространстве могут быть скрещивающимися. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.

Способы задания прямой в пространстве.

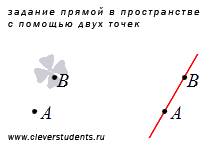
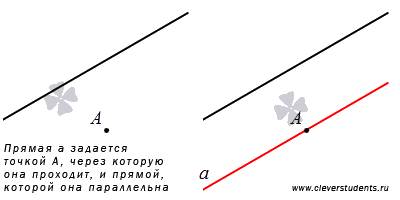
Второй способ задания прямой в пространстве основан на теореме: через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и причем только одна.

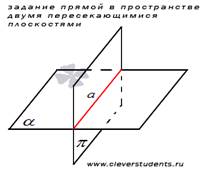
Следующий способ задания прямой в пространстве основан на аксиоме стереометрии: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Еще один способ задания прямой в пространстве следует из теоремы: если задана плоскость и не лежащая в ней точка, то существует единственная прямая, проходящая через эту точку и перпендикулярная к заданной плоскости.