Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.
Скалярное произведение векторов 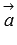 и
и 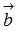 будем обозначать как
будем обозначать как  . Тогда формула для вычисления скалярного произведения имеет вид
. Тогда формула для вычисления скалярного произведения имеет вид 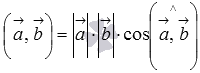 , где
, где 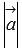 и
и 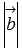 - длины векторов
- длины векторов 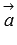 и
и 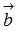 соответственно, а
соответственно, а 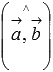 - угол между векторами
- угол между векторами 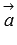 и
и 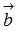 .
.
Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то 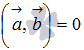 .
.
Вектор можно скалярно умножить на себя. Скалярное произведение вектора на себя равно квадрату его длины, так как по (скалярный квадрат).
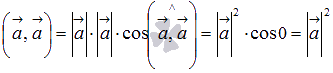
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов 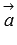 и
и 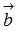 .
.
То есть, для векторов 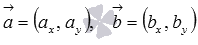 на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид
на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид
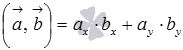 ,
,
а для векторов 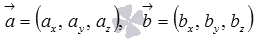 в трехмерном пространстве скалярное произведение в координатах находится как
в трехмерном пространстве скалярное произведение в координатах находится как
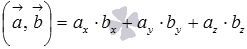 .
.
Таким образом, мы имеем третье определение скалярного произведения. Покажем, что это определение эквивалентно первому.
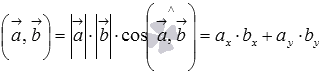
 2015-04-30
2015-04-30 1372
1372
