1. 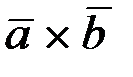 = -
= - 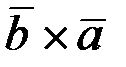 .
.
2. 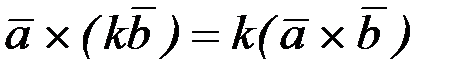 .
.
3. 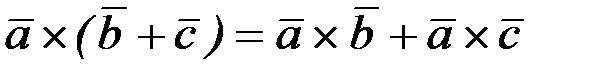 .
.
Векторное произведение ортов
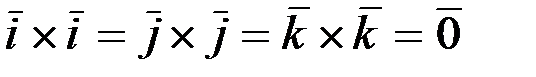 .
.
 |
| Рис. 1 |
движение осуществляется слева направо,
то знак векторного произведения положи-
тельный, в противном случае – отрицательный,
т.е. 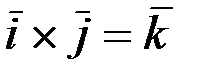 ,
, 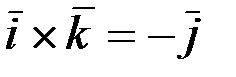 и тд.
и тд.
Если заданы два вектора 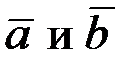 своими координатами в ортонормированном базисе как
своими координатами в ортонормированном базисе как 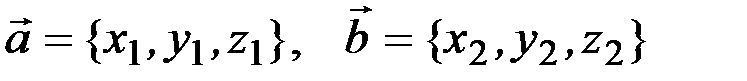 , то
, то 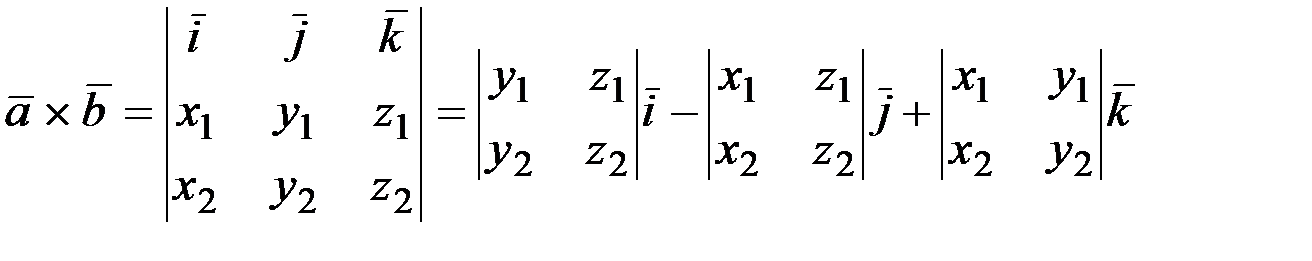 .
.
Применение векторного произведения
1. Площадь треугольника, построенного на векторах 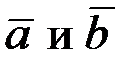 , равна
, равна 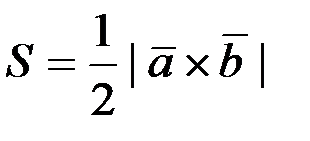 .
.
2. Условие коллинеарности двух векторов 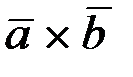 =
=  .
.
3. Момент силы 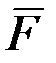 , приложенный в точке А, равен
, приложенный в точке А, равен 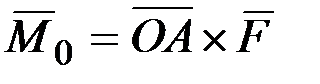 .
.
________________
2.3.1. Построить векторы 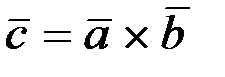 , если 1)
, если 1) 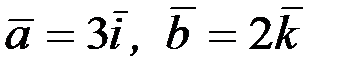 ;
;
2) 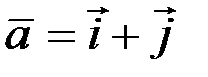 и
и 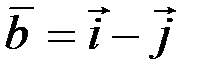 .
.
Ответ: 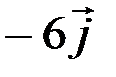 ; 0.
; 0.
2.3.2. Раскрыть скобки и упростить выражения:
1) 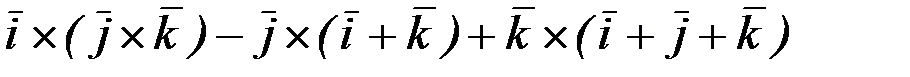 ;
;
2) 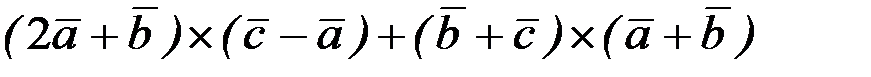 .
.
Ответ: 1) 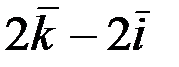 ; 2)
; 2) 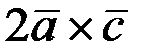 .
.
2.3.3. Даны векторы 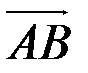 =
= 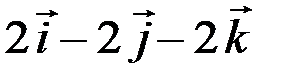 ,
, 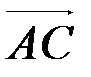 =
= 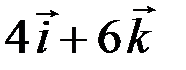 . Найти
. Найти 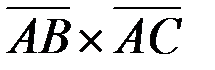 .
.
Ответ: 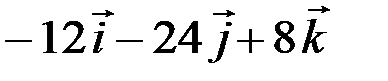 .
.
2.3.4. Даны векторы 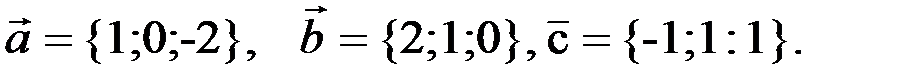 Найти
Найти 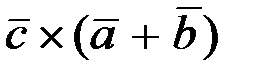 .
.
Ответ: 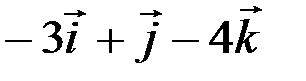 .
.
2.3.5. Найти площадь треугольника с вершинами А(1;2;0); В(3;0;-3); С(5;2;6).
Ответ:14.
2.3.6. Найти площадь параллелограмма, построенного на векторах 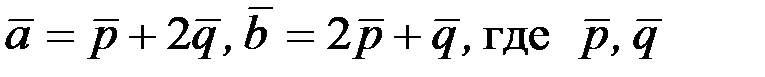 - единичные векторы, угол между которыми равен π/3.
- единичные векторы, угол между которыми равен π/3.
Ответ: 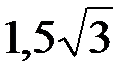 .
.
2.3.7. Найти площадь параллелограмма, диагоналями которого служат векторы 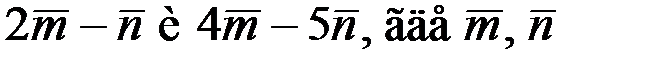 - единичные векторы, образующие угол 45°.
- единичные векторы, образующие угол 45°.
Ответ: 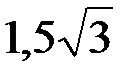 .
.
2.3.8. Сила 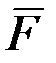 =
= 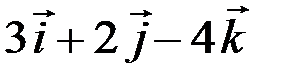 приложена в точке М(2;-1;1). Найти ее момент относительно начала координат.
приложена в точке М(2;-1;1). Найти ее момент относительно начала координат.
Ответ: 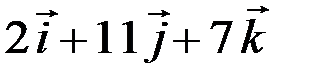 .
.
2.3.9. Построить векторы 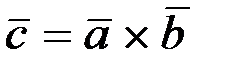 , если 1)
, если 1) 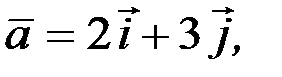
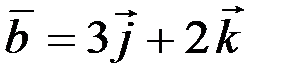 ; 2)
; 2) 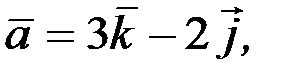
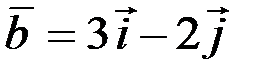 .
.
Ответ: 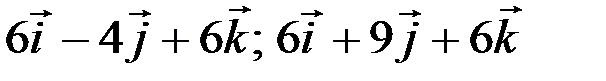 .
.
2.3.10. Раскрыть скобки и упростить выражения:
1) 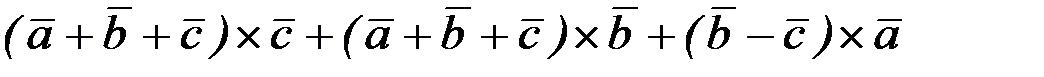 ;
;
2) 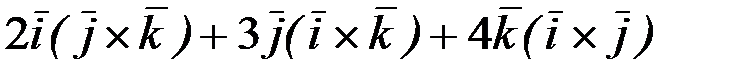 .
.
Ответ: 1) 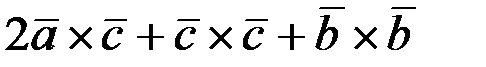 ; 2) 3.
; 2) 3.
2.3.11. Даны векторы 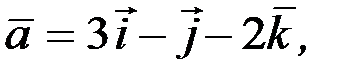
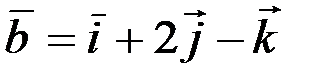 . Найти векторное произведение
. Найти векторное произведение 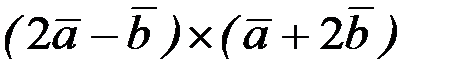 .
.
Ответ: 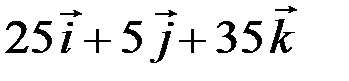 .
.
2.3.12. Дан треугольник с вершинами А(2;-1;2); В(1;2;-1); С(3;2;1). Найти его площадь.
Ответ: 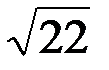 .
.
2.3.13. Найти площадь параллелограмма, построенного на векторах 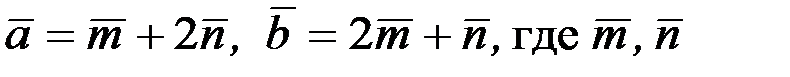 - единичные векторы с углом между ними 30°.
- единичные векторы с углом между ними 30°.
Ответ: 1,5.
 2015-04-20
2015-04-20 740
740








