1. 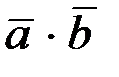 =
= 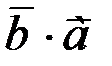 .
.
2. 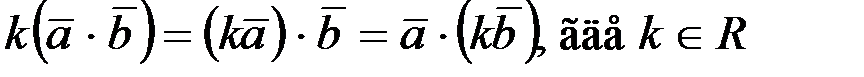 .
.
3. 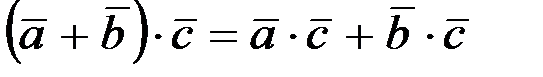 .
.
4. Если скалярное произведение двух ненулевых векторов равно нулю, то 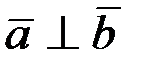 .
.
5. Скалярный квадрат вектора равен квадрату его модуля, то есть 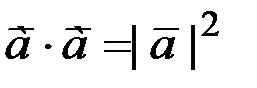 .
.
Скалярное произведение ортов:
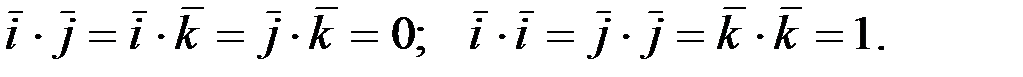 .
.
Если векторы 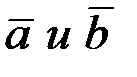 заданы своими координатами в ортонормированном базисе как
заданы своими координатами в ортонормированном базисе как 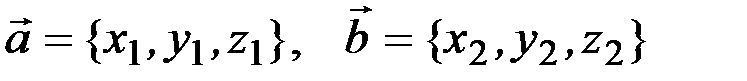 ,то
,то 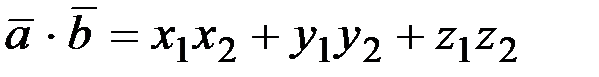 .
.
Применение скалярного произведения
1. Длина вектора 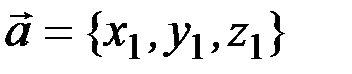 равна
равна 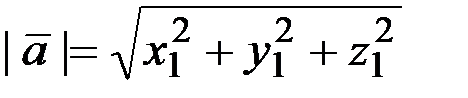 .
.
2. Угол между векторами 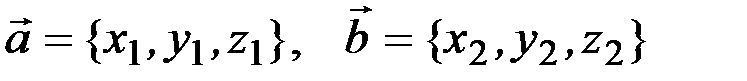 определяется как
определяется как 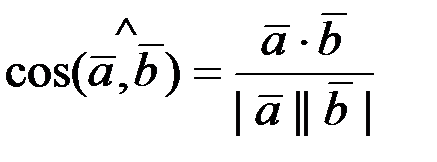 .
.
3. Проекция вектора 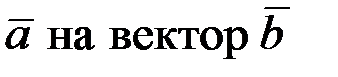 :
: 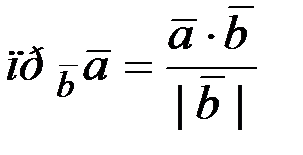 .
.
4. Условие ортогональности двух векторов 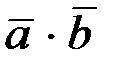 =0,
=0, 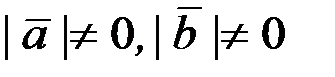 .
.
5. Работа силы 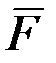 по перемещению материальной точки из А в В равна
по перемещению материальной точки из А в В равна 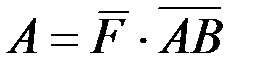 .
.
______________
2.2.1. Найти скалярное произведение 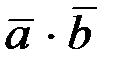 векторов
векторов 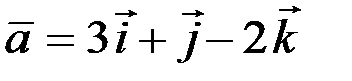 и
и 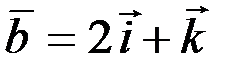 .
.
Ответ: 4.
2.2.2. Найти угол между векторами 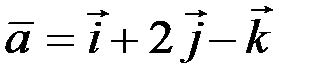 и
и 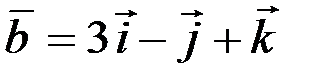 .
.
Ответ: 90°.
2.2.3. Найти алгебраическую проекцию вектора 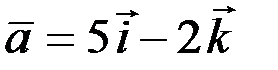 на вектор
на вектор 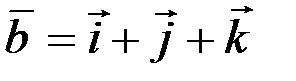 .
.
Ответ: Ö3.
2.2.4. Даны векторы 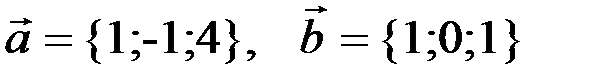 . Вектор
. Вектор 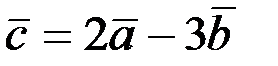 . Найти:
. Найти: 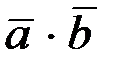 ;
; 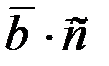 ;
; 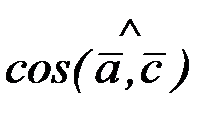 ;
; 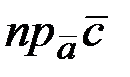 ;
; 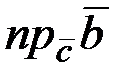 .
.
Ответ: 5; 4; 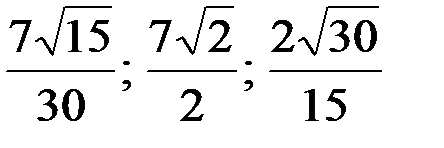 .
.
2.2.5. Даны векторы: 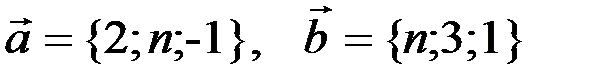 . При каких значениях n угол между векторами
. При каких значениях n угол между векторами 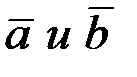 тупой, прямой, острый?
тупой, прямой, острый?
Ответ: n < 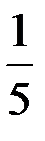 ; n =
; n = 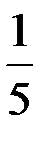 ; n >
; n > 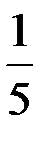 .
.
2.2.6. Вычислить работу силы 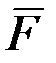 ={3;2;4}, если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7).
={3;2;4}, если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7).
Ответ: А=6.
2.2.7. На материальную точку действуют силы 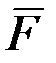 1=
1= 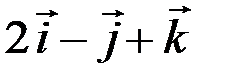 ,
, 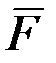 2=
2= 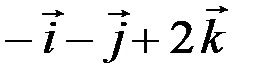 ,
, 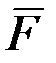 3=
3= 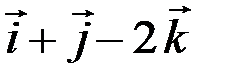 . Найти работы равнодействующей этих сил и силы
. Найти работы равнодействующей этих сил и силы 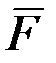 2 при перемещении точки из А(2;-1;0) в В(4;1;-1).
2 при перемещении точки из А(2;-1;0) в В(4;1;-1).
Ответ:1; -6.
2.2.8. Определить длину вектора 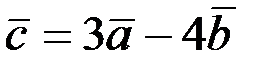 , если
, если 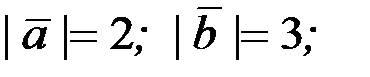
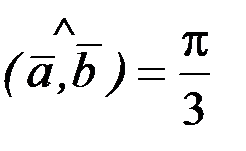 .
.
Ответ: 6Ö3
2.2.9. Определить длины диагоналей параллелограмма, построенного на векторах 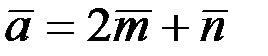 и
и 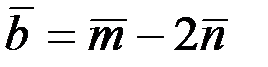 , где
, где 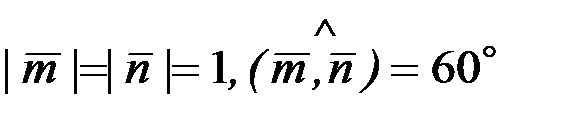 .
.
Ответ: Ö7; Ö13.
2.2.10. Векторы 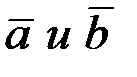 взаимно перпендикулярны, а вектор
взаимно перпендикулярны, а вектор 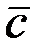 образует с ними углы, равные π/3. Зная, что
образует с ними углы, равные π/3. Зная, что 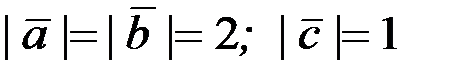 , найти
, найти 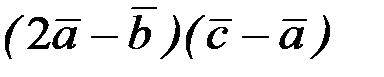 .
.
Ответ: -7.
_____________
2.2.11. Даны векторы 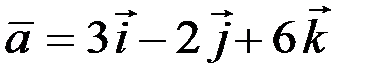 и
и 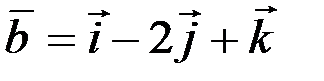 . Найти
. Найти 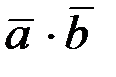 ,
, 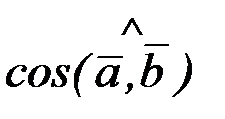 ,
, 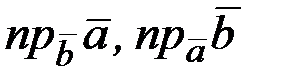 .
.
Ответ: 13; 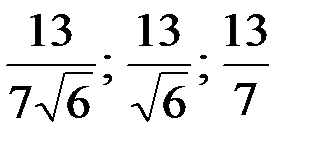 .
.
2.2.12. Даны векторы 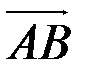 =
= 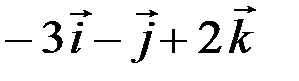 ,
, 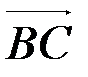 =
= 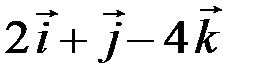 ,
, 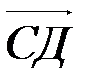 =
= 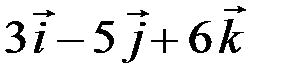 . Найти модуль скалярного произведения диагоналей четырехугольника АВСД.
. Найти модуль скалярного произведения диагоналей четырехугольника АВСД.
Ответ:
2.2.13. Даны векторы 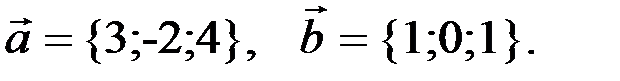 Вектор
Вектор 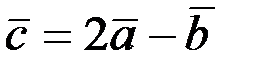 . Найти:
. Найти: 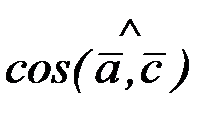 ,
, 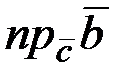 .
.
Ответ: 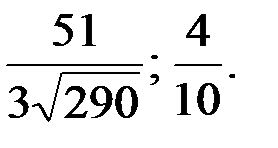
2.2.14. Даны силы 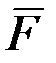 1=
1= 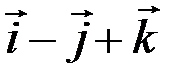 ,
, 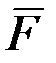 2=
2= 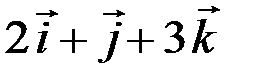 . Найти работу их равнодействующей при перемещении точки из начала координат в точку А(2;-1;-1).
. Найти работу их равнодействующей при перемещении точки из начала координат в точку А(2;-1;-1).
Ответ: 2.
2.2.15. Найти угол между векторами 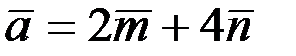 и
и 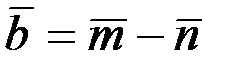 , где
, где 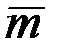 и
и 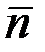 - единичные векторы с углом между ними 120°.
- единичные векторы с углом между ними 120°.
Ответ: -1/2.
 2015-04-20
2015-04-20 1135
1135
