Некоторые пояснения

4.1.Комплексное сопротивление идеальной индуктивности L является чисто мнимым числом с аргументом +90° (или -90°, когда индуктивность является отрицательной):

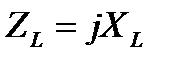. (4.3)

Здесь X_L – индуктивное сопротивление, которое пропорционально частоте:

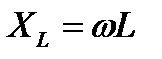(4.4)

Индуктивное сопротивление индуктивности совпадает с ее реактивным сопротивлением

X (X = Х_L). (4.5)

4.2.Индуктивность L обычно реализуется индуктивностью катушки индуктивности. Реальная катушка индуктивности при протекании токов приводит к рассеянию энергии.

Потери энергии в реальной катушке индуктивности можно учесть последовательной схемой замещения, в которой последовательно с идеальной индуктивностью включено резистивное сопротивление потерь R_L(рис. 11).

Комплексное сопротивление реальной катушки индуктивное L имеет не только мнимую, но и вещественную составляющие:

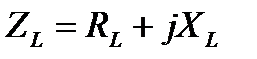(4.6)

Рис.11 Последовательная схема замещения катушки индуктивности.

При этом индуктивность 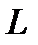и сопротивление 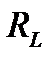потерь приведенной схемы замещения зависят от частоты. Это затрудняет анализ соответствующих цепей в широком диапазоне частот. Поэтому были найдены квазиэквивалентные схемы, которые достаточно точно реализуют характеристики реальной катушки индуктивности в широком диапазоне частот. Одна из таких схем (рис. 12) с тремя независящими от частоты параметрам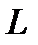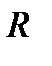и , и 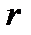обычно достаточно точно передает свойства реальных катушек индуктивности в диапазоне радиочастот.

Рис.12 – схема с тремя независящими от частоты параметрам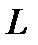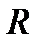и , и,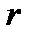

3. При анализе экспериментальной цепи рис. 8 на фиксированной в ходе эксперимента частоте воспользуемся последовательной схемой замещения реальной катушки индуктивности (рис. 10).

Пользуясь последней схемой цепи и найденными экспериментальными значениями 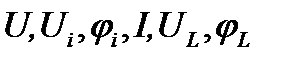не представляет проблем построить векторную диаграмму токов и напряжений экспериментальной цепи (рис. 12).

Эта диаграмма построена при дополнительном предположении, что начальная фаза тока равна -90°. Поэтому под указанным углом вначале были отложены в некотором.масштабе совпадающие по фазе комплексы 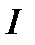и 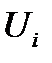. Затем построен с учетом найденного фазового сдвига комплекс 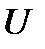. И, наконец, с учетом своего фазового сдвига, - вектор, соответствующий комплексу .

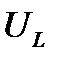Проекции из конца последнего вектора на вертикальную и горизонтальную оси определили размер векторов, соответствующих комплексам 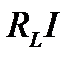и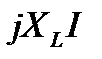

После расчета по построенной диаграмме значений величин 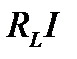и 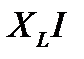и подсчета 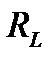и 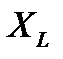,может быть рассчитано экспериментальное значение индуктивности катушки:

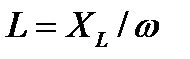(4.6)

Контрольные вопросы к лабораторной работе.

1. Что такое индуктивное сопротивление и как оно связано с реактивным и комплексным сопротивлениями индуктивности?

2. Как зависит реактивное сопротивление индуктивности от частоты?

3. Нарисуйте треугольник сопротивлений последовательной RL-цепи.

4. Чему равны активная, реактивная, полная и комплексная мощности в идеальной индуктивности?

5. Нарисуйте последовательную схему замещения реальной индуктивности с одним резистором, позволяющую учесть потери на некоторой частоте.

6. Нарисуйте последовательную схему замещения реальной индуктивности с двумя резисторами, позволяющую учесть потери в диапазоне радиочастот

Список литературы

Основная литература

1. Запасный А.И. Основы теории цепей: Учебное пособие – М: РИОР, 2006 – 336с.

2. В.П.Попов. Основы теории цепей. Учебник для ВУЗов – М: Высшая школа, 2007 – 576с.

3. В. П. Бакалов, В. Ф. Дмитриков, Б. И. Крук. Основы теории цепей Для высших учебных заведений – М: Горячая Линия - Телеком, 2009 – 600с.

4. В. В. Фриск Основы теории цепей – М: РадиоСофт 2002 – 192с.

Дополнительная литература

5. Г. И. Атабеков Учебники и учеб. пособ.д/ высшей школы(ВУЗы). – М: Лань Изд-во 2009 – 424с.

6. С. И. Баскаков. Лекции по теории цепей – М: Едиториал УРСС 2009 – 280с.

Учебное издание