Нечеткие знания. Виды нечеткости знаний. Модели представления нечетких знаний

Корректные задачи часто можно решить существующими методами систематизации и программирования. В области некорректных задач точные знания нельзя получить

Знания, извлеченные из экспертов, как правило, содержат различные виды так называемых НЕ-факторов – нечетких знаний.

Они могут проявляться в умолчаниях, неточных сравнениях, подсознательных знаниях и др., но для представления таких знаний в БЗ требуется конкретная формализация.

Все нечеткости можно классифицировать: Недетерминированность выводов, Многозначность, Ненадежность, Неполнота, Неточность.

Недетерминированное управление выводом наиболее харак­терно для систем искусственного интеллекта. Таким образом, возникает необходимость определения пути, по кото­рому следует начать поиск в первую очередь.

Алгоритм А. Поисковая задача сформулирована как задача поиска в пространстве состояний пути от исходного состояния заданной задачи до целевого состояния путем повторения возможных преобразований.

Задача Нильсона:.); на поле 3 x 3 размещены восемь пронумерованных шашек, цель игры — от заданного начального состоя­ния перейти к целевому состоянию так, как показано ниже:

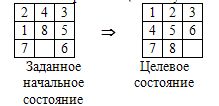На поле один пустой квадрат: состояние можно изменить, передвигая шашку сверху, снизу, справа или слева на пустой квадрат. Следовательно, в этой игре есть четыре оператора преобразования состоя­ния и до четырех степеней свободы квадрата или шашек, соответствующие одному из передвижений шашки на пустой квадрат, будем перемещать пустой квадрат:

перемещение пустого квадрата влево (при этом слева есть квадрат);

перемещение пустого квадрата вверх (при этом вверху есть квадрат);

перемещение пустого квадрата вправо (при этом справа есть квадрат);

перемещение пустого квадрата вниз (при этом внизу есть квадрат)

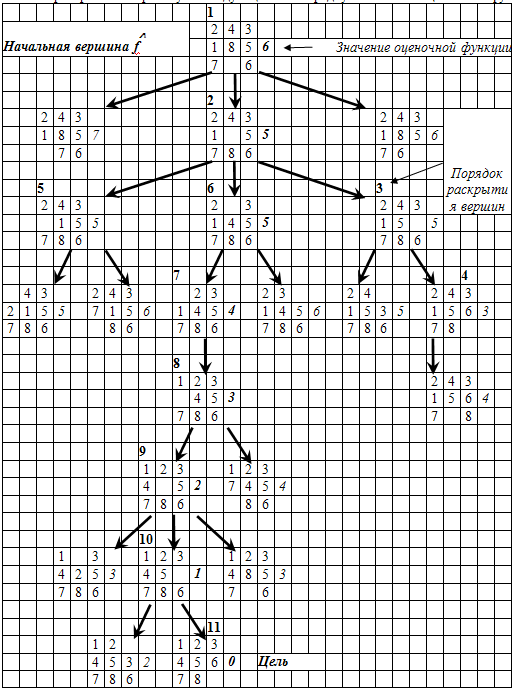Зададим оценочную функцию f(n) - стоимость оптимального пути к цели от первой вершины (нач. состояния) через n вер­шин дерева поиска: f(n) = g(n) + h(n),

где g(n) - стоимость оптимального пути от 1-ой вершины до n -й вершины,

h(n) - стоимость оптимального пути от n -й вер­шины до цели.

Будем считать, что перемещение 1 шашки имеет стоимость 1, а до цели ведет оптимальный путь с минимальной стоимостью.

Пусть априорное значение оценочной функции (т.к.точное значение f(n) в процессе игры знать не возможно): f’(n)=g(n)+h’(n),

где h’(n) — априорное значение h(n) – количесво фишек, стоящих не на своих местах. g(n) — это глубина от 1-ой вершины до n -й вершины.

Выбираем вершину с наименьшим из значений оценочной функ­ции, применяем оператор и раскрываем вершину, затем создаем до­черние вершины (при этом не возвращаемся к уже появившимся вершинам). Повторяем эту процедуру, до целевого состояния.

Если на каком-либо шаге встречаем h_i’(n) >h’_i-1(n), товозвращаемся на шаг назад и раскрываем вершину со следующим по порядку значением оценочной функции.

Многозначность. Многозначность интерпретации — обычное явле­ние при понимании естественных языков и распозна­вании изображений и речи. Устранить многозначность в зависимости от типа информации можно более широким контекстом и семантическими ограничениями.

Модель доски объявлений. Фреймовая модель со слотами с понижением рангов. Семь уровней интерпретации от звуков к слогам, словам, группам слов и фразам, многознач­ность интерпретации на каждом уровне устраняется путем согласования с верхними уровнями, на основе модели доски объявлений; интерпретация не всегда однознач­на и обычно генерируются несколько гипотез. Интерпретируем от низшего к высшему (от аку­стических параметров звуковых волн до понимания смысла вопроса).

Метод релаксации (метод систематического устранения многозначности при интерпретации изображений с помощью циклических операций) Одним из этапов распознавания предмета яв­ляется интерпретация физического смысла линий. Для каждой грани при этом можно указать, что она вы­пукла (помечена знаком «+»), вогнута (помечена знаком «–») или является граничной (помечена зна­ком ®, справа от стрелки — видимая поверхность):Маркируем одну из граней у вершины; фильтруем – расставляем метки для остальных граней, интерпретируя известные метки.