Переход из газообразного состояния в жидкое

Экспериментальные изотермы

Голландский ученый Ван Марум еще в XVIII веке, занимаясь проверкой применимости закона Бойля-Мариотта к газу аммиаку в широком диапазоне температур и давлений, установил удивительную закономерность. Производя изотермическое сжатие газа в сосуде под поршнем, он обнаружил, что достигая некоторого определенного давления (в его опыте около 7 атм), изотермический процесс сжатия становится также и изобарическим: 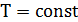, 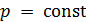. Изотерма на диаграмме 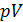образует «полочку» (рис. 13.3). Все точки этой полочки за исключением самых крайних соответствуют двухфазному состоянию. В них газ и жидкость сосуществуют в состоянии термодинамического равновесия. В точке 1 и при более низких давлениях всё вещество находится в газообразной фазе, а в точке 2 и при более высоких давлениях всё вещество находится в жидкой фазе.

В XIX веке экспериментальными исследованиями перехода вещества из газообразного состояния в жидкое занимались многие ученые, из них наиболее успешно Каньяр де ля Тур, Дмитрий Иванович Менделеев, Томас Эндрюс, Майкл Фарадей, Хейке Камерлинг Оннес. Эксперименты с самыми разными веществами показали следующее.

В семействе изотерм для одного и того же вещества наблюдается уменьшение изобарного участка с ростом температуры пока при некоторой температуре, называемой критической температурой, изобарный участок графика («полочка») не превратится в точку (на рис. 13.3 она обозначена буквой К). Эта точка называется критической точкой. Она соответствует критическому состоянию вещества при давлении 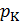и объеме 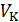. Изотерма 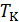, разумеется, называется критической изотермой. Заметим, что понятие критической температуры было введено Менделеевым в 1860 году.

В критическом состоянии вещества нет различий между жидкостью и газом. Это состояние в научной литературе иногда называют флюидным. Оно обладает многими интересными свойствами, в дальнейшем мы их подробно обсудим. Сейчас же отметим, что при 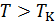все изотермы идут монотонно (на рис. 13.3 это 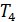и 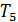) и соответствуют исключительно газообразному состоянию. Последнее означает, что невозможно перевести газ в жидкое состояние с помощью изотермического сжатия, если его температура выше .

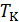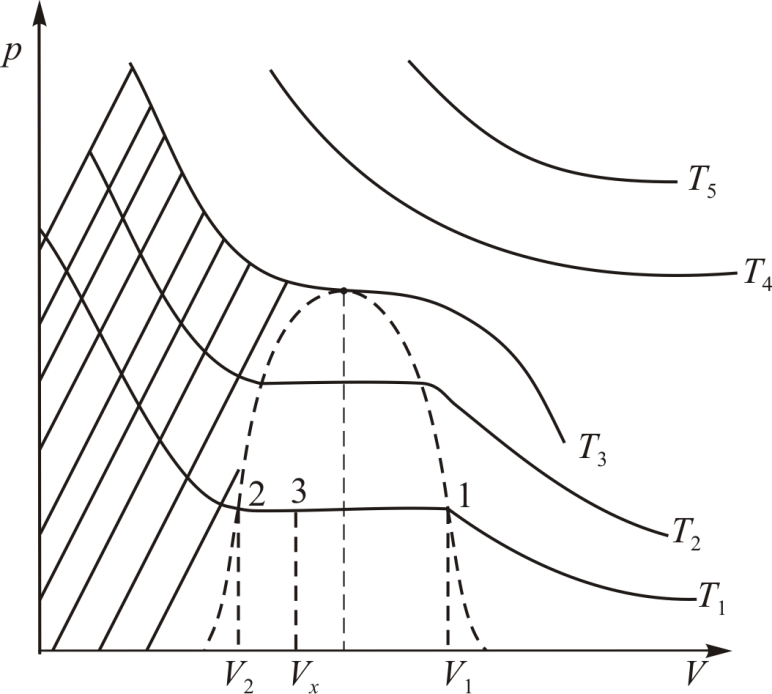
Рис. 13.3.

По графику изотермы двухфазного состояния (рис. 13.3) можно определить массы 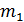и 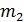жидкой и газообразной фаз в любой точке 3 на изобаре 2-3-1, используя правило рычага и закон сохранения массы 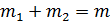. Правило рычага выражается равенством

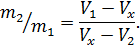
Понимание всех закономерностей, наблюдающихся в экспериментах по сжижению газов возможно только на основе термического уравнения состояния реального газа.

13.4. Уравнения состояния реального газа

Любое уравнение состояния, полученное либо из первых принципов, либо на полуэмпирический основе, дающее функциональную зависимость 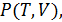должно прежде всего отвечать двум требованиям:

1.Условие механической устойчивости выполняется во всей области значени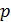й и 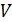, а именно

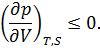
2.В предельном случае, когда 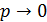, уравнение состояния реального газа 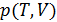переходит в уравнение Клапейрона – Менделеева

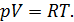
Если уравнение состояния отвечает этим требованиям, то его подвергают экспериментальной проверке, если нет, то возможны два варианта: его исправляют или от него отказываются.

Существует несколько десятков уравнений состояния реального газа, полученных на полуэмпирической основе и адекватно описывающих их свойства. Некоторые из них приведены на схеме 13.4.1. Наибольшее признание в современной научной практике имеют уравнения Редлиха - Квонга, Пенга -Робинсона и их модификации. Параметры 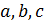и прочие, фигурирующие в уравнениях на схеме 13.4.1, имеют в каждом уравнении свой определенный смысл и значение. Кроме того, они различны для разных газов и могут быть получены из эксперимента.

Самое первое уравнение реального газа было предложено известным голландским физиком Ван-дер-Ваальсом в 1873 году. Уравнение Ван-дер-Ваальса имеет простую и физически ясную структуру, позволяющую сравнительно легко получать результаты в аналитической форме. Поэтому в дальнейшем мы будем часто прибегать именно к этому уравнению для описания свойств реальных газов и жидкостей.

Схема 13.4.1

Уравнения состояния реальных газов

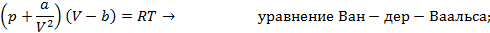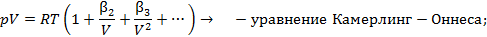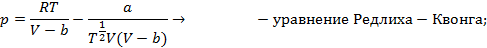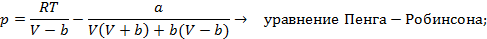13.5. Модель газа Ван-дер-Ваальса. Уравнение Ван-дер-Ваальса

В теории Ван-дер-Ваальса используется упрощенная модель межмолекулярного взаимодействия в газе. На рис. 13.4 можно сравнить реальный потенциал типа Леннарда-Джонса (13.6) и потенциал Ван-дер-Ваальса, изображенный пунктирной линией.

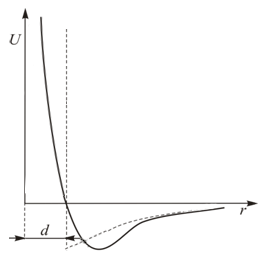Как видно из рисунка, часть кривой 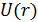заменяется вертикальной прямой. Если 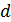– расстояние до этой прямой от начала координат, то центры взаимодействующих частиц не могут сблизиться на расстояние меньшее 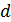, что соответствует модели твердых упругих шаров. Именно эта модель находит свое отражение в уравнении состояния газа Ван-дер-Ваальса. Запишем это уравнение и рассмотрим его внимательно.

Рис. 13.4.

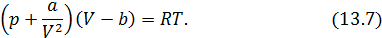
Невооруженным глазом видно, что оно может быть получено небольшим изменением уравнения Клапейрона-Менделеева. Действительно, отталкивание молекул в модели газа Ван-дер-Ваальса учтено только наличием собственного объема молекул. Это приводит к уменьшению свободного объема, предоставленного молекулам на некоторую величину 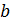. Как показывает детальное рассмотрени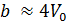е , где 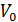– объем молекул данного газа в количестве 1 моль. Разумеется, поправка 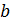для каждого газа имеет свое значение. Таким образом, смысл выражения, заключенного во вторых скобках уравнения (13.7) становится явным.

Теперь обратим внимание на выражение в первых скобках (13.7). К давлению газа добавилась поправка, связанная с наличием сил притяжения между молекулами газа. Вспомните, как мы вычисляли давление идеального газа на стенку сосуда через изменение импульса молекул, налетающих на стенку. В реальном газе импульс налетающих молекул изменяется не только под действием сил давления со стороны стенки, но и под действием сил, с которыми их тянут внутрь газа молекулы пристеночного слоя.

Поэтому давление газа можно представить как сумму двух вкладов

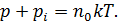
Слагаемое 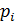называется внутренним, или молекулярным давлением. Внутреннее давление пропорционально силе, действующей на молекулу пристеночного слоя, а также числу молекул в нем, отнесенное к единице площади. Каждое из названных сомножителей пропорционально концентрации частиц 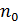. Следовательно

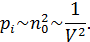
Предполагая, что количество молекул газа равно 1 молю, можно записать

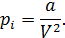
Теперь, надеюсь, вам стал ясен смысл всех составляющих уравнения (13.7).

Заметим, что вывод уравнения (13.7) был осуществлен с учетом условий:

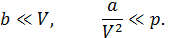
Кроме того, актуально предположение, что молекулы газа сферически симметричны, поскольку используется модель твердых упругих шаров.

В заключение запишем уравнение Ван-дер-Ваальса для произвольного числа 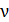молей

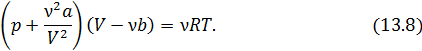
На следующей лекции мы покажем, как применять уравнение Ван-дер-Ваальса для описания различных свойств реальных газов.

Контрольные вопросы

1. Какие соотношения между средними значениями кинетической энергии и энергии межатомных взаимодействий молекул характерны для газов, жидкостей и твердых тел?

2. Чем отличаются аморфные тела от кристаллических тел?

3. Какие операции симметрии применимы к твердому телу?

4. Что называется а) вектором трансляции, б) решеткой Браве, в) сложной решеткой, г) ячейкой Браве?

5. Объясните причину анизотропии кристаллов.

6. Что называется энергией связи кристалла. Каков интервал изменения этой величины?

7. Какие типы химической связи характерны для кристаллов? Приведите примеры соединений на каждый тип связи.

8. При каких условиях модель идеального газа становится неприменимой к газообразному состоянию вещества? Какие эксперименты позволяют судить об этом?

9. Какова природа молекулярных сил, действующих в реальных газах и жидкостях? Изобразите примерный график потенциала Леннарда-Джонса. Сравните его с потенциалом Ван-дер-Ваальса.

10. Выделите характерные особенности изотермического перехода из газообразного состояния в жидкое.

11. Каким двум требованиям должно отвечать термическое уравнение состояния, реального газа полученное либо из первых принципов, либо на полуэмпирической основе.

12. Запишите уравнение Ван-дер-Ваальса. Объясните физический смысл поправок к давлению и объему.

ЛЕКЦИЯ 14

СВОЙСТВА РЕАЛЬНЫХ ГАЗОВ. РЕЗУЛЬТАТЫ ТЕОРИИ

ВАН-ДЕР-ВААЛЬСА И ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ.

14.1. Изотермы газа Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса позволяет построить теоретические изотермы реального газа и сравнить их с соответствующими экспериментальными изотермами (рис. 13.3). Уравнение (13.7) можно записать в виде

Если считать температуру 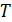постоянной, то (14.1) будет уравнением изотермы. Семейство теоретических изотерм представлено на рис. 14.1.

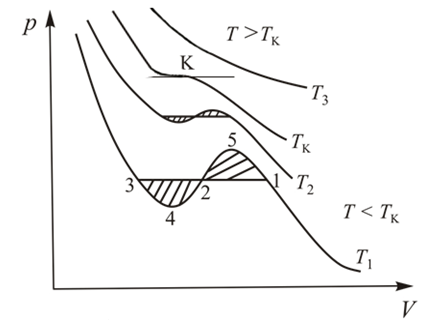
Рис. 14.1.

Как видно из этого рисунка при 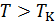изотермы имеют вид монотонных кривых, что согласуется с видом экспериментальных изотерм на рис. 13.3. в том же температурном диапазоне. Критическая изотерма по своему виду тоже совпадает с экспериментальной критической изотермой. А вот изотермы при 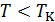существенно отличаются от экспериментальных прототипов. Каждая кривая содержит волнообразный участок и именно на том месте, где соответствующая экспериментальная изотерма превращается в изобару (полочку). Обратите внимание, что на участке изотермы 4-2-5 все точки соответствуют неустойчивым состояниям вещества, поскольку на этом участке не выполняется условие механической устойчивости (12.27).

В самом деле, в этой области с увеличением объема 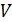растет и давление 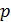, условие антибатного изменения параметров нарушено, а это значит, что ни одно из обозначенных состояний не может быть практически реализовано. Поэтому теоретическую изотерму следует исправить: «вырезать» участок возрастающей кривой 4-2-5 и воспроизвести изобарическую двухфазную область в виде отрезка горизонтальной прямой 3-2-1 (рис. 14.1).

Возникает вопрос, как проводить эту прямую? Повыше или пониже? Оказывается, положение горизонтального участка изотермы можно определить с помощью термодинамического равенства Клаузиуса

Применим это равенство к квазистатическому циклическому процессу 1-2-3-4-2-5-1. Так как этот процесс изотермический, то (14.2) принимает вид 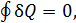а поскольку 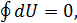то равенство Клаузиуса переходит в равенство 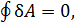или .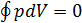

Отсюда становится ясно, что прямую 3-2-1 надо провести так, чтобы заштрихованные площади криволинейных фигур 1-2-5-1 и 2-3-4-2 на рис. 14.1 были равны. Это правило называется правилом Максвелла.

Закончив исправление изотермы Ва-дер-Ваальса, выясним смысл оставленных «веточек» 3-4 и 1-5. Отмеченные участки изотермы отвечают критерию механической устойчивости. Соответствующие им состояния вещества могут быть реализованы при выполнении специальных условий. Эти состояния называются метастабильными. Участок 1-5 представляет пересыщенный пар, а участок 3-4 – перегретую жидкость. Обе фазы обладают ограниченной устойчивостью. При малейшем возмущении вещества в этих состояниях происходит его распад на две устойчивые фазы: жидкость и её насыщенный пар.

Метастабильные состояния вещества находят применение в приборах, предназначенных для наблюдения траектории движения заряженной микрочастицы. Пересыщенный пар используется в камере Вильсона, а перегретая жидкость в пузырьковой жидководородной камере. Заряженная частица, проходя через вещества в этих камерах, оставляет за собой цепочку ионов. В камере Вильсона на этой цепочке ионов происходит конденсация пара и образуется след (трек) частицы из капелек жидкости. В пузырьковой камере возникшие ионы становятся центрами парообразования, поэтому след пролетевшей частицы отмечается пузырьками водорода.

14.2. Критическое состояние вещества

Как вы помните, к понятию критического состояния вещества нас привел анализ экспериментальных изотерм. Для того, чтобы разобраться в сущности критических явлений и понять, как они связаны с уравнением состояния и условиями устойчивости термодинамического равновесия, обратимся к уравнению Ван-дер-Ваальса. Не потому, что это уравнение очень точное, а потому, что оно простое и «модельное».

Прежде всего, займемся нахождением критических параметров 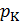, , 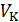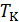. Это можно сделать двумя способами.

Первый способ основан на конкретной математической структуре уравнения Ван-дер-Ваальса. Это уравнение третьей степени относительно 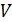. В критической точке оно принимает вид

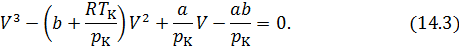
Поскольку в критическом состоянии все три корня уравнения совпадают и равны 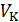, то (14.3) должно приводиться к виду

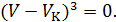
Возведем в куб выражение в скобках и приравняем коэффициенты при одинаковых степенях 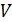в полученном уравнении и уравнении (14.3). Получим три уравнения, связывающие критические параметры и постоянные , .

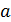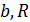Второй способ основан на использовании математических свойств точки 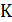на критической изотерме (рис. 14.1). Отметим, что второй способ является более универсальным. Этим способом можно вычислить критические параметры на основе любого уравнения состояния реального газа (Схема 13.4.1). Математические свойства критической точки таковы:

• Она является точкой перегиба изотермы, поэтому в ней

• Касательная в этой точке горизонтальна, следовательно

Исходя из уравнения изотермы (14.1), вычислим первую и вторую производные от давления по объему. Решая совместно (14.4), (14.5) и (14.1), найдем критические параметры. Тем и другим способом из уравнения Ван-дер-Ваальса получаются следующие выражения для критических параметров

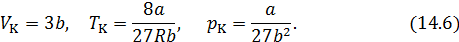
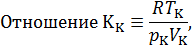
называется критическим коэффициентом. В теории Ван-дер-Ваальса согласно (14.6) критический коэффициент равен

Как видно, его значение не зависит от природы газа, что не соответствует действительности. Опыт показывает, что критические коэффициенты для реальных газов имеют различные значения в интервале 3,0 ÷ 4,5. Использование более точных уравнений состояния вещества позволяет получить лучшее согласие теоретических значений критических параметров с экспериментальными результатами. Значения критических величин для некоторых газов приведены в табл. 14.2.1.

Таблица.14.2.1.

Вещество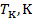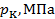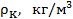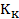
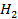	33,2	1,28		3,03
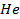	5,2	0,23		3,13
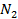		3,35		3,42
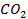		7,3		4,49

На основании (14.6) можно записать

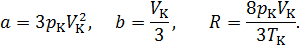
Таким образом, полученные из эксперимента и критические параметры могут быть использованы для нахождения постоянных 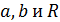. Молярная газовая постоянная 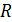в критическом состоянии обозначается как 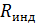(индивидуальная). Оказывается, что для различных веществ она разная, но всегда меньше чем 8,31 Дж/моль∙ 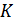. Например, для водорода 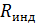= 6,76 Дж/моль∙ 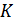, а для водяного пара 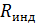= 5,01 Дж/моль∙ 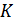. Такое поведение газовой постоянной находит следующее объяснение.

Поскольку 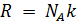, где 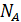– число структурных элементов в моле, то получается, что в критическом состоянии происходит уменьшение структурных единиц. Действительно, молекулы вещества в критическом состоянии слипаются, объединяются в комплексы, которые при удалении от критического состояния распадаются, и 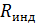становится равной универсальной газовой постоянной. Следует иметь в виду, что при анализе явлений вблизи критического состояния необходимо использовать значение .

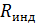Закон соответственных состояний

Если в качестве единиц измерения объема, давления и температуры использовать критические значения этих величин, то перейдем к безразмерным величинам, которые называются приведенными параметрами:

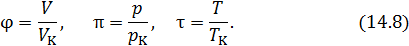
Уравнение состояния, записанное в этих переменных, называется приведенным уравнением состояния. Приведенные уравнения состояния одинаковы для всех веществ. Это положение называется закономсоответственных состояний. Конкретный вид уравнения состояния не имеет значения. В качестве примера запишем приведенное уравнение состояния Ван-дер-Ваальса

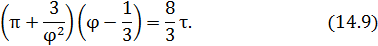
Уравнение (14.9) не содержит никаких индивидуальных констант вещества и описывает состояния всех газов, к которым применимо уравнение Ван-дер-Ваальса.

Закон соответственных состояний позволяет по известному поведению одних веществ, предсказывать поведение других. Это обстоятельство сыграло большую роль в конце XIX и в начале ХХ века при исследованиях условий сжижения газов. В частности удалось оценить температуру и давление, при которых возможно сжижение водорода.

Свойства вещества в критическом состоянии

В критическом, или флюидном, состоянии вещества многие его свойства ведут себя аномально. Судите сами. Обращаются в нуль такие параметры как динамическая вязкость 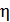, поверхностное натяжение 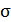и скрытая теплота парообразования 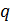. Принимают бесконечно большие значения такие величины как теплоемкост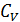и и 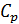, а также термический коэффициент сжатия 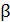. Поведение сжимаемости вещества объясняется тем, что в критической точке

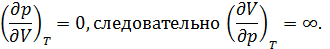
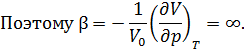
Поразительная способность к сжатию приводит к заметному распределению плотности вещества по высоте под действием собственного веса. Так относительное изменение плотности гептана в критическом состоянии (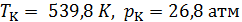) на интервале высот в 6 см составляет около 35%.

Другой особенностью вещества в критическом состоянии является медленность установления равновесного состояния. Характерное время релаксации для того же гептана составляет сутки и более. Вблизи критического состояния велика роль флуктуаций плотности, поскольку отсутствует механизм выравнивания неоднородностей распределения вещества в пространстве, ведь

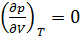. Это значит, что локальное возрастание плотности не приводит к возрастанию давления в этом месте, в отличие от того как это происходит вдали от критического состояния.

Убедиться в том, что флуктуации плотности велики в критическом состоянии можно опытным путем, наблюдая явление, которое называется критической опалесценцией. Для демонстрации этого эффекта надо заполнить эфиром немного более трети запаянной прочной стеклянной ампулы. Процесс нагревания эфира можно наблюдать на экране с помощью проекционного фонаря. Сначала видны две фазы: светлая – газ (пар), более темная – жидкость. Затем наблюдается процесс кипения жидкости и увеличение объема газообразной фазы. Выше 180⁰ С мениск исчезает, и ампула оказывается заполненной однородной средой – эфиром выше критической температуры. На экране будет видна светлая (прозрачная) ампула. После чего нагревание следует прекратить. Ампула с эфиром начнет медленно остывать в естественных условиях. Когда её температура опустится до величины близкой к критической на экране появится изображение абсолютно черной ампулы, которое довольно быстро исчезнет и снова появится мениск разделяющий жидкость и пар. Поглощение и рассеяние света на флуктуациях плотности вещества вблизи критического состояния объясняет наблюдающееся помутнение, называемое опалесценцией.

Анализ применения уравнения Ван-дер-Ваальса