Уравнение Ван-дер-Ваальса

Из всего сказанного вытекает, что уравнение, правильно описывающее поведение газов при больших плотностях, должно учитывать, во-первых, взаимное притяжение молекул друг к другу и, во-вторых, конечную величину собственного объема молекул.

Из большого числа уравнений, предложенных для описания поведения реальных газов, самым простым и вместе с тем дающим достаточно хорошие результаты оказалось уравнение Ван-дер-Ваальса. Это уравнение получено путем внесения поправок в уравнение pV_KM =. = RT и имеет следующий вид:

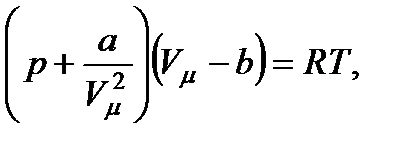(29)

где р — давление, оказываемое на газ извне (равное давлению газа на стенки сосуда), а и b — константы Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем. Если давление выражено в ньютонах на квадратный метр, а объем – в кубических метрах на киломоль, то константа а имеет размерность н • м⁴/кмоль², а константа b — м³/кмоль. Иногда константу а выражают в am*л^2/ моль², а константу b— в л/моль.

Константа b определяет ту часть объема, которая недоступна для движения молекул вследствие их конечных размеров. Эта константа равна учетверенному объему молекул, что вытекает из следующих соображений. Пусть в сосуде имеется лишь две молекулы. Центр любой из этих молекул не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра молекулы d. Таким образом, для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы. В расчете на одну молекулу недоступным оказывается объем, равный учетверенному объему молекулы. Поскольку молекулы, как правило, сталкиваются попарно (вероятность столкновений трех и более молекул крайне мала), приведенное рассуждение справедливо для любой пары молекул. Отсюда следует, что в расчете на каждую из молекул газа недоступным будет объем, равный четырем объемам одной молекулы, а для всех молекул — объем, равный учетверенному суммарному объему молекул.

Поправка a/V²_μ дает внутреннее давление p_i, обусловленное взаимным притяже­нием молекул друг к другу. Если бы взаимодействие между молекулами вдруг прекратилось, то для того, чтобы удержать газ в пределах того же объема, понадо­билось бы увеличить внешнее давление на величину, равную внутреннему давле­нию p_i. Обратная пропорциональность p_i квадрату объема объясняется следующими причинами. Вследствие быстрого убывания сил притяжения между молекулами с увеличением расстояния между ними, начиная с некоторого расстояния r, взаимодействием между молекулами можно вполне пренебречь. Расстояние r называется радиусом молекулярного действия. Сферу радиуса r называют сферой молекулярного действия. Проведем мысленно плоскость в газе (рис. 8) и попытаемся оценить силу, с которой притягивают друг друга части газа,лежащие по обе стороны от этой плоскости. Отнеся эту силу к единице поверхности, мы получим внутреннее давление.

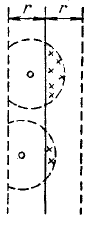
Рис.8. Внутреннее давление в газе

Каждая из молекул, находящихся слева от воображаемой плоскости, испытывает притяжение со стороны тех молекул, находящихся справа от плоскости, которые попадают в пределы выступающей за плоскость части сферы молекулярного действия, описанной вокруг данной молекулы (эти молекулы обозначены на рис. 6 крестиками). Число таких молекул, а следовательно, и сила, действующая на каждую из молекул, лежащих слева от плоскости, пропорциональны числу молекул в единице объема п. Притяжение со стороны молекул, находящихся справа от плоскости, испытывают только те молекулы, находящиеся слева от плоскости, которые попадают в слой толщины r. Число этих молекул также пропорционально п. Таким образом, сила, с которой одна часть газа притягивает другую, а следовательно, и внутреннее давление оказываются пропорциональными п². Поскольку n обратно пропорционально объему газа, внутреннее давление будет обратно пропорционально квадрату объема.

Уравнение (29) написано для одного киломоля газа. Чтобы перейти к уравнению для произвольной массы газа m, соответствующей zкиломолей газа (z = m/μ), нужно учесть, что z киломолей при тех же условиях за­нимают в z раз больший объем: V = zVμ. Заменяя в (29) V через Vμ/z, получаем:

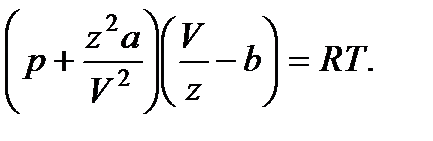
Умножив это уравнение на z и введя обозначения

а' = z2a; b' = zb, (30)

приходим к уравнению Ван-дер-Ваальса для z молей:

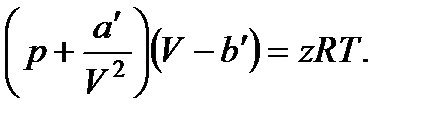(31)

Буквами а' и b' обозначены константы Ван-дер-Ваальса для z киломолей. Их связь с а и b дается соотношениями (30). Размерность а' равна н*м⁴, константа b' имеет размерность объема.

Насколько уравнение Ван-дер-Ваальса лучше передает поведение газов, чем уравнение (5), можно судить по данным, приведенным в таблице 1. В третьем столбце таблицы даны значения величины 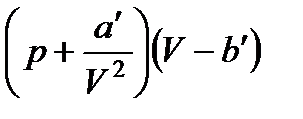для той жемассы азота, для которой даны во втором столбце значения pV. Согласно (31), эта величина должна оставаться постоянной. Как видно из таблицы, уравнение Ван-дер-Ваальса гораздо лучше согласуется с экспериментом, чем уравнение (5).

В соответствии с тем фактом, что все реальные газы с уменьшением плотности приближаются по своим свойствам к идеальному газу, уравнение Ван-дер-Ваальса в пределе, при стремлении объема к бесконечности переходит в уравнение (5). В этом можно убедиться, вынеся в уравнении (31) р и V за скобки:

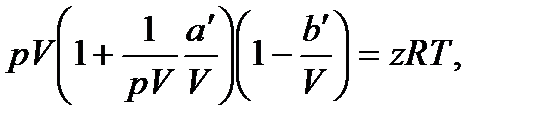
и учитывая, что произведение pV остается примерно постоянным.

Раскрыв скобки в уравнении (31) и умножив получившееся выражение на V², уравнение Ван-дер-Ваальса можно привести к виду

pV³ – (b'p zRT)V2+ а'V = а'b' (32)

Получилось кубическое уравнение относительно V, коэффициенты которого зависят от параметров р и Т. Кубическое уравнение со свободным членом и вещест­венными коэффициентами имеет три решения, причем в зависимости от соотношения между коэффициентами либо все три решения будут вещественными, либо одно решение — вещественным, а два — комплексными. Поскольку объем может быть только вещественным, комплексные решения не имеют физического смысла.