Методы вычислений

Методические указания для студентов I курса

Базей Александр Анатольевич

Одесса 2008

ЛИТЕРАТУРА

1 Хемминг Р.В. Численные методы для научных работников и инженеров. – М.: Наука, 1968. – 400 с.

2 Блажко С.Н. Курс сферической астрономии. – Москва, Ленинград, ОГИЗ, 1948. – 416 с.

3 Щиголев Б.М. Математическая обработка наблюдений. – М.: Наука, 1969. – 344 с.

4 Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. – М.: Наука, 1977. том I, том II – 400 с.

5 Худсон Д. Статистика для физиков. – М.: Мир, 1967. – 244 с.

6.Берман Г.Н. Приемы счета. – Москва, 1953. – 88 с.

7.Румшинский Л.З. Математическая обработка результатов эксперимента. – Москва, Наука 1971. – 192 с.

8.Калиткин Н.Н. Численные методы. – Москва, Наука 1978. – 512 с.

9.Фильчаков П.Ф. Численные и графические методы прикладной математики. – Киев, «Наукова думка», 1970. – 800 с.

10.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, т.1-3. – Москва, Наука 1966.

СОДЕРЖАНИЕ

Приближенные вычисления 2

О построении графиков

Сглаживание 10

Аппроксимация 12

Спрямление (линеаризация) 13

Метод наименьших квадратов 15

Интерполирование 24

Интерполяционный полином Лагранжа 26

Остаточный член формулы Лагранжа 29

Интерполяционный полином Ньютона для таблицы с переменным шагом 30

Интерполирование по таблице с постоянным шагом 34

Интерполяционнные полиномы Стирлинга, Бесселя, Ньютона 37

Интерполирование по таблице функции двух аргументов 42

Дифференцирование по таблице 44

Численное решение уравнений 46

Дихотомия (метод деления пополам) 46

Метод простых итераций 47

Метод Ньютона 50

Поиск минимума функции одной переменной 51

Метод золотого сечения 51

Метод парабол 54

Вычисление определенного интеграла 56

Формула трапеций 59

Формула средних или формула прямоугольников 61

Формула Симпсона 62

Решение обыкновенных дифференциальных уравнений. Задача Коши 64

Классический метод Эйлера 66

Уточненный метод Эйлера 67

Метод прогноза и коррекции 69

Методы Рунге-Кутта 71

Гармонический анализ 74

Ортогональные системы функций 78

Метод 12 ординат 79

ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ

Решим простую задачу. Допустим, что студент живет на расстоянии 1247 м от вокзала. Поезд отходит в 17 часов 38 мин. За сколько времени до отхода поезда студент должен выйти из дому, если его средняя скорость равна 6 км/час?

Решение получаем сразу:

.

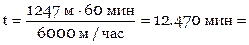
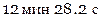Однако вряд ли в действительности кто-либо стал бы пользоваться этим математически точным решением и вот почему. Вычисления выполнены совершенно точно, но точно ли измерено расстояние до вокзала? Можно ли вообще измерить путь пешехода, не допустив никаких погрешностей? Может ли пешеход передвигаться по строго определенной линии в городе, где полно людей и автомобилей, которые перемещаются во всевозможных направлениях? А скорость 6 км/час – разве она определена абсолютно точно? И так далее.

Вполне понятно, что каждый отдаст предпочтение в данном случае не «математически точному», а «практическому» решению этой задачи, то есть прикинет, что идти 12-15 минут и прибавит еще несколько минут для гарантии.

Для чего же в таком случае вычислять секунды и их доли и стремиться к такой степени точности, которой нельзя воспользоваться на практике?

Математика наука точная, но понятие «точности» само требует уточнения. Для этого надо начинать с понятия числа, поскольку от точности чисел, от достоверности исходных данных в значительной мере зависит точность результатов вычислений.

Источников получения чисел есть три: счет, измерения и выполнение различных математических операций

Если количество пересчитываемых предметов невелико и если оно постоянно во времени, то мы будем получать абсолютно точные результаты. Например, на руке 5 пальцев, в ящике 300 подшипников. Иначе обстоит дело, когда говорят: в Одессе в 1979 году было 1000 000 жителей. Ведь люди рождаются и умирают, приезжают и уезжают; число их все время меняется даже за тот промежуток времени, в течение которого выполнен счет. Поэтому на самом деле имеется в виду, что жителей было около 1 000 000, может быть 999125, или 1001263, или еще какое-нибудь число, близкое к 1 000 000. В этом случае 1 000 000 дает приближенное число жителей города.

Любое измерение нельзя выполнить абсолютно точно. Каждый прибор дает какую-либо погрешность. Кроме того, два наблюдателя, измеряя одним и тем же прибором одну и ту же величину, обычно получают несколько различные результаты, полное же совпадение результатов является редким исключением.

Даже такой простейший измерительный прибор, как линейка, имеет «ошибку прибора» - ребра и плоскости линейки несколько отличаются от идеальных прямых и плоскостей, штрихи на линейке не могут быть нанесены на абсолютно равных расстояниях, да и сами штрихи имеют определенную толщину; так что при измерении мы не можем получить результаты более точные, чем толщина штрихов.

Если вы измерили длину стола и получили значение 1360.5 мм, то это вовсе не значит, что длина стола ровно 1360.5 мм – если этот стол измерит другой или вы повторите измерение, то можно получить значение и 1360.4 мм, и 1360.6 мм. Число 1360.5 мм выражает длину стола приближенно.

Математические операции также не все можно выполнить без ошибок. Извлечь корень, найти синус или логарифм, даже разделить не всегда можно абсолютно точно.

Все без исключения измерения приводят к приближенным значениям измеряемых величин. В некоторых случаях измерения проводятся грубо, тогда получаются большие погрешности, при тщательных измерениях погрешности получаются меньше. Абсолютная точность при измерениях не достигается никогда.

Рассмотрим теперь вторую сторону вопроса. Нужна ли на практике абсолютная точность и какую ценность представляет приближенный результат?

При расчете линии электропередачи или газопровода никто не будет определять расстояние между опорами с точностью до миллиметра или диаметр трубы с точностью до микрона. В технике и строительстве каждую деталь или сооружение можно изготовить только в пределах определенной точности, которая определяется так называемыми допусками. Эти допуски колеблются от частей микрона до миллиметров и сантиметров, в зависимости от материала, размера и назначения детали или сооружения. Следовательно, для определения размеров детали не имеет никакого смысла вести вычисления с точностью большей, чем та, которая необходима.

Итак:

1) Исходные данные для вычислений, как правило, имеют погрешности, то есть являются приближенными;

2) Эти погрешности, часто увеличенными, переходят в результаты вычислений. Но практика и не требует точных данных, а довольствуется результатами с некоторыми допустимыми погрешностями, величина которых должна быть наперед заданной.

3) Обеспечить необходимую точность результата можно только тогда, когда исходные данные будут достаточно точными и когда учитываются все погрешности, которые привносятся самими вычислениями.

4) Вычисления с приближенными числами надо выполнять приближенно, стремясь при решении задачи достигнуть минимальной затраты труда и времени.

Обычно в технических расчетах допустимые погрешности находятся в пределах от 0.1 до 5%, но в научных вопросах они могут быть снижены до тысячных долей процента. Например, при запуске первого искусственного спутника Луны (31 марта 1966 г.) стартовая скорость около 11200 м/сек должна была быть обеспечена с точностью до нескольких сантиметров в секунду, чтобы спутник вышел на окололунную, а не околосолнечную орбиту.

Заметим, кроме того, что правила арифметики выведены в предположении, что все числа точные. Поэтому, если вычисления с приближенными числами выполнять как с точными, то создается опасное и вредное впечатление точности там, где ее в действительности нет. Истинная научная, и, в частности, математическая точность состоит именно в том, чтобы указать на наличие почти всегда неизбежных погрешностей и определить их пределы.