Положение материальной точки в выбранной системе координат определяется радиус-вектором 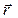 . Вектор
. Вектор 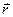 можно разложить на его составляющие по осям координат
можно разложить на его составляющие по осям координат
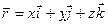 , (1.1)
, (1.1)
где 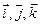 - единичные вектора, направленные вдоль коорди- натных осей; x, y, z – координаты точки (рис.1.1).
- единичные вектора, направленные вдоль коорди- натных осей; x, y, z – координаты точки (рис.1.1).
При движении материальной точки по произвольной траектории ее положение описывается векторным кинемати- ческим уравнением движения
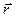 =¦(t),
=¦(t),
либо тремя скалярными кинематическими уравнениями
x = f(t), y = f(t), z = f(t).
Если за некоторый промежуток времени D t = t2 - t1 точка переместилась из положения 1, определяемого радиуc-векто- ром 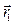 , в положение 2, определяемое радиус-вектором
, в положение 2, определяемое радиус-вектором 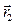 , то вектор
, то вектор 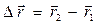 называется вектором перемещения и характеризует изменение пространственного положения точки за данный промежуток времени. Длина траектории DS, заключенная между точками 1 и 2, представляет собой путь, пройденный за тот же промежуток времени D t.
называется вектором перемещения и характеризует изменение пространственного положения точки за данный промежуток времени. Длина траектории DS, заключенная между точками 1 и 2, представляет собой путь, пройденный за тот же промежуток времени D t.
Для характеристики быстроты и направления движения материальной точки вводят понятие скорости. Вектор средней скорости представляет собой вектор перемещения за единицу времени
< 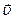 > =
> = 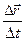 (1.2)
(1.2)
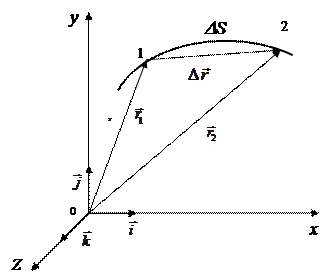 |
Рис.1.1
Вектор мгновенной скорости определяется первой производной радиус-вектора по времени
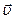 =
= 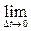
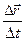 =
=  =
= 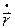 . (1.3)
. (1.3)
Направление вектора скорости совпадает с направлением касательной к траектории движения в данной точке.
Разложение вектора 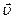 в декартовой системе координат имеет вид:
в декартовой системе координат имеет вид:
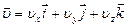 . (1.4)
. (1.4)
При этом, проекции скорости точки на оси координат равны первым производным по времени от соответствующих
координат
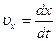 ;
; 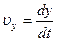 ;
; 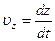 , (1.5)
, (1.5)
а модуль вектора скорости равен
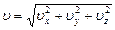 . (1.6)
. (1.6)
Модуль вектора скорости может быть также определен через производную пути по времени
u =ú 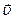 ú =
ú = 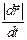 =
= 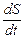 =
= 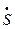 . (1.7)
. (1.7)
Если известен вид функции u (t), то путь, пройденный точкой за определенный промежуток времени, определяется интегрированием
S = 
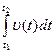 . (1.8)
. (1.8)
На графике зависимости скорости от времени u = f (t) он выражается площадью заштрихованной фигуры (рис.1.2).
Быстроту изменения скорости материальной точки в пространстве характеризует вектор ускорения:
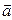 =
= 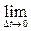
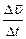 =
= 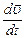 =
= 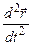 . (1.9)
. (1.9)
Ускорение, таким образом, есть первая производная вектора скорости по времени, или вторая производная радиус - вектора по времени.
Проекция ускорения на оси координат равны производ- ным по времени от соответствующих проекций скорости или вторым производным по времени от соответствующих координат точки:
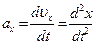 ,
, 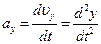 ,
, 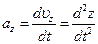 (1.10)
(1.10)
В общем случае, направление вектора 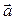 составляет некоторый угол a с направлением скорости
составляет некоторый угол a с направлением скорости 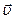 , поэтому вектор
, поэтому вектор 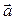 можно разложить на две взаимно перпендикулярные составляющие (рис.1.3).
можно разложить на две взаимно перпендикулярные составляющие (рис.1.3).
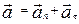 . (1.11)
. (1.11)
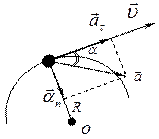
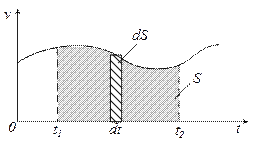
Рис.1.2 Рис.1.3
Вектор 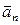 совпадает с направлением нормали в данной точке траектории и называется нормальным (центростреми- тельным) ускорением.
совпадает с направлением нормали в данной точке траектории и называется нормальным (центростреми- тельным) ускорением.
Нормальное ускорение характеризует изменение векто- ра скорости только по направлению. Его величина равна
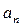 =
= 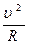 , (1.12)
, (1.12)
где R – радиус кривизны траектории в данной точке.
Вектор 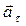 - тангенциальное (касательное) ускорение, характеризующее изменение скорости по величине. Значение тангенциального ускорения определяется выражением
- тангенциальное (касательное) ускорение, характеризующее изменение скорости по величине. Значение тангенциального ускорения определяется выражением
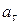 =
= 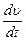 . (1.13)
. (1.13)
Уравнения скорости и пути для прямолинейного равно- переменного движения (равноускоренного и равнозамедлен- ного) в проекции на координатную ось имеют следующий вид:
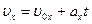 , (1.14)
, (1.14)
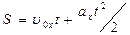 . (1.15)
. (1.15)
Приведём в качестве примера кинематические уравне- ния движения тела, брошенного под углом к горизонту (рис.1.4).

Рис.1.4
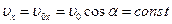 ;
;
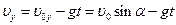 ;
;
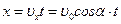 ;
;
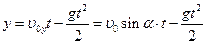 .
.
Решение данной системы уравнений позволяет определить время полёта, максимальную высоту подъёма и дальность полёта:
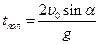 ;
;
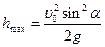 ;
;
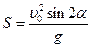 .
.
 2015-05-14
2015-05-14 1096
1096
