2015-05-14
2638
1) Для нахождения уравнения траектории движения частицы необходимо исключить параметр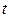 
из кинематиче- ских уравнений:
.
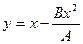Полученное уравнение представляет собой уравнение параболы.
2) Вектор скорости частицы в момент времени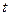 
определяется выражением:
,
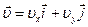где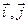 
- единичные векторы вдоль осей Х и У, а 
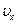и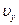 
- проекции вектора скорости на соответствующие оси.
Дифференцируя уравнения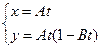 
по времени, получим:
; 
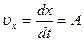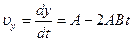
и, следовательно,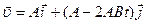 
.
Модуль вектора скорости равен
.
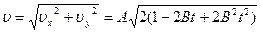Вектор ускорения представляет собой первую производ- ную от вектора скорости
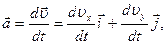
где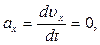 
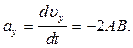
Следовательно,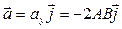 
.
Знак «-» в полученном выражении свидетельствует о том, что ускорение направлено в сторону, противоположную оси У.
Модуль ускорения равен
.
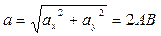3) Вектор средней скорости определяется выражением
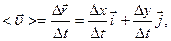
где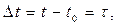 
поскольку 
, 
.
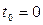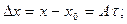
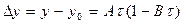Окончательно,
.
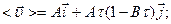
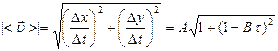Пример 2. Камень брошен с вышки в горизонтальном направлении со скоростью υ = 30 м/c. Определить скорость, тангенциальное и нормальное ускорение камня в конце третьей секунды после начала движения.
