В соответствии с законом сохранения момента импульса для системы шарик-стержень будет иметь
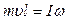 , (1)
, (1)
где I -момент инерции стержня относительно оси вращения. По теореме Штейнера
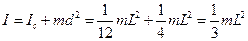 .
.
С учетом этого уравнение (1) приводится к виду
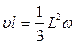 .
.
При абсолютно упругом ударе выполняется закон сохране- ния механической энергии, в соответствии с которым
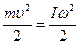 , (2)
, (2)
или после преобразования
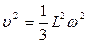 . (3)
. (3)
Решая систему уравнений (1) и (3), найдем
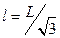 .
.
Пример 5. Человек стоит на скамье Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамейки. Стержень служит осью колеса, расположенного на верхнем конце стержня. Скамья неподвиж- на, колесо вращается с частотой ν’ = 10 с-1. Радиус колеса равен 20 см, его масса m = 3 кг. Определить частоту вращения ν1 скамьи, если человек повернёт стержень на угол 1800. Суммарный момент инерции человека и скамьи I = 6 кг·м2.
 2015-05-14
2015-05-14 1805
1805








