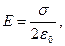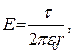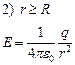Для графического изображения электрических полей применяют силовые линии (линии напряжённости).
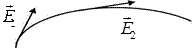 Линии напряжённости – это линии, касательные к которым в каждой точке совпадают с направлением вектора
Линии напряжённости – это линии, касательные к которым в каждой точке совпадают с направлением вектора 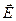 (рис. 4.3).
(рис. 4.3).
Рис.4.3
Силовые линии электрического поля не замкнуты, они начинаются на положительных зарядах и оканчиваются на отрицательных, они непрерывны и не пересекаются.
Густота линий напряжённости выбирается так, чтобы количество линий, пронизывающих единичную площадку, перпендикулярную силовым линиям, было равно числовому значению вектора 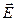 .
.
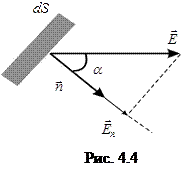 Рассмотрим некоторую поверхность S, пронизываемую силовыми линиями электрического поля. На этой поверхности выделим элементарную площадку dS, нормаль
Рассмотрим некоторую поверхность S, пронизываемую силовыми линиями электрического поля. На этой поверхности выделим элементарную площадку dS, нормаль 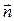 к которой образует угол a с вектором
к которой образует угол a с вектором 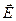 в окрестности этой площадки (рис.4.4).
в окрестности этой площадки (рис.4.4).
Число линий 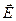 , пересекаю- щих данную площадку, равно
, пересекаю- щих данную площадку, равно
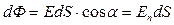 ,
,
где 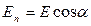 - проекция вектора
- проекция вектора 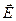 на нормаль к площадке.
на нормаль к площадке.
Величина dФ называется потоком вектора 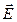 сквозь элементарную площадку dS. Полный поток через поверх- ность S определяется путём интегрирования по заданной поверхности
сквозь элементарную площадку dS. Полный поток через поверх- ность S определяется путём интегрирования по заданной поверхности
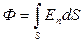 . (4.12)
. (4.12)
Физический смысл потока: Ф - число пересечений силовых линий с данной поверхностью.
 Поток вектора
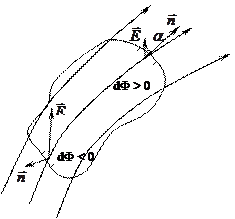
Поток вектора 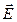 есть величина алгебраическая, знак его зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверх- ность S. В случае замкнутых поверхностей под нормалью к dS понимается обращенная наружу, т.е. внешняя нормаль. Поэтому в тех местах, где вектор
есть величина алгебраическая, знак его зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверх- ность S. В случае замкнутых поверхностей под нормалью к dS понимается обращенная наружу, т.е. внешняя нормаль. Поэтому в тех местах, где вектор 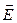 направлен наружу (т.е. силовые линии выходят из объема, охватываемого поверхно- стью)
направлен наружу (т.е. силовые линии выходят из объема, охватываемого поверхно- стью) 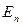 и соответственно dФ положительны, где вектор
и соответственно dФ положительны, где вектор 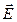 направлен внутрь - поток dФ будет отрицателен (рис.4.5). Поток вектора
направлен внутрь - поток dФ будет отрицателен (рис.4.5). Поток вектора 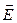 сквозь произвольную замкнутую поверхность зависит только от алгебраиче- ской суммы зарядов, охватываемых этой поверхностью.
сквозь произвольную замкнутую поверхность зависит только от алгебраиче- ской суммы зарядов, охватываемых этой поверхностью.

Теорема Гаусса для электростатического поляв вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверх- ности зарядов, деленной на 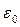 .
.
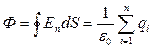 . (4.13)
. (4.13)
Теорему Гаусса используют для расчета симметричных электрических полей.
В таблице приведены формулы расчета напряжённостей некоторых симметричных полей, полученные с помощью теоремы Гаусса.
| № п/п | Электрическое поле | Формулы напряженности | Графики | ||||||
| Поле равномерно заряженной бесконечной плоскости |
где s - поверхностная плотность заряда | 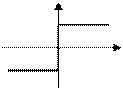
| |||||||
| Поле бесконечно длинной равномерно заряженной нити |
r - расстояние от нити, t - линейная плотность заряда |
E
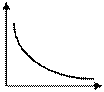 r r
| |||||||
| Равномерно заряженная сферическая поверхность |
где R - радиус сферы, r - расстояние от центра сферы. | 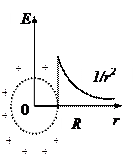
| |||||||
| Продолжение таблицы | |||||||||
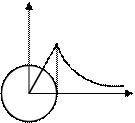
| Поле объемно заряженного шара | 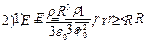 где R - радиус шара,
r - расстояние от центра шара,
r - объёмная плотность заряда где R - радиус шара,
r - расстояние от центра шара,
r - объёмная плотность заряда
|
|
 2015-05-14
2015-05-14 614
614