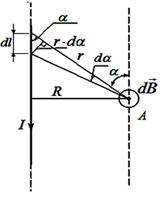
Пусть по прямому тонкому бесконечно длинному проводнику течет постоянный электрический ток, как показано на рис. 2. вычислим индукцию магнитного поля в произвольной точке А, находящейся от оси проводника на расстоянии 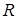 . Для этого проводник разобьем на множество малых элементов длиной
. Для этого проводник разобьем на множество малых элементов длиной 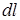 . Выберем произвольно один такой элемент. Этот элемент
. Выберем произвольно один такой элемент. Этот элемент 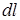 проводника с током
проводника с током 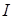 создает в точке А магнитное поле, вектор магнитной индукции
создает в точке А магнитное поле, вектор магнитной индукции 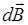 которого, согласно закону Био-Савара-Лапласа, равен
которого, согласно закону Био-Савара-Лапласа, равен
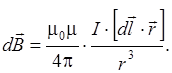
Вектор 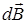 в точке А направлен перпендикулярно плоскости чертежа к нам. Модуль этого вектора равен Рис.2. Магнитное поле прямого тока Idl
в точке А направлен перпендикулярно плоскости чертежа к нам. Модуль этого вектора равен Рис.2. Магнитное поле прямого тока Idl
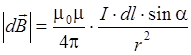 . (2)
. (2)
В выражении (2) имеется две переменные величины 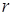 и
и 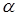 . Преобразуем выражение (2) так, чтобы в него входила только одна переменная –
. Преобразуем выражение (2) так, чтобы в него входила только одна переменная – 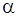 . Для этого выразим
. Для этого выразим 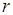 и
и 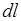 через угол
через угол 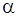 .
.
Из рис.2 находим:
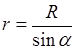 ,
, 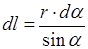 .
.
Подставив эти значения в выражение (2) и произведя преобразования, получим дифференциал искомой величины как функцию одной переменной:
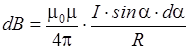 . (3)
. (3)
Легко видеть, что все векторы  от элементов проводника с током в точке А коллинеарны между собой и одинаково направлены, следовательно, результирующую индукцию магнитного поля найдем интегрированием выражения (3), где угол
от элементов проводника с током в точке А коллинеарны между собой и одинаково направлены, следовательно, результирующую индукцию магнитного поля найдем интегрированием выражения (3), где угол  изменяется в пределах от
изменяется в пределах от 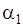 до
до 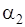 . Так как проводник бесконечно длинный, то
. Так как проводник бесконечно длинный, то 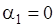 , а
, а 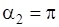 . Следовательно
. Следовательно
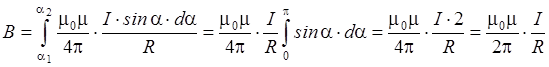 .
.
Таким образом, магнитная индукция поля прямолинейного бесконечно длинного проводника с током, находящегося в изотропной среде, определяется формулой (4):
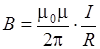 . (4)
. (4)
Закон Ампера — закон взаимодействия электрических токов. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила 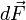 , с которой магнитное поле действует на элемент объёма
, с которой магнитное поле действует на элемент объёма 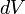 проводника с током плотности
проводника с током плотности 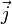 , находящегося в магнитном поле с индукцией
, находящегося в магнитном поле с индукцией 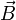 :
:
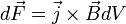 .
.
Если ток течёт по тонкому проводнику, то 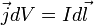 , где
, где 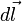 — «элемент длины» проводника — вектор, по модулю равный
— «элемент длины» проводника — вектор, по модулю равный 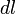 и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Сила 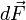 , с которой магнитное поле действует на элемент , с которой магнитное поле действует на элемент 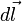 проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока 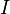 в проводнике и векторному произведению элемента длины в проводнике и векторному произведению элемента длины 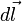 проводника на магнитную индукцию проводника на магнитную индукцию 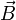 : : 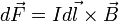 . . |
Направление силы 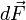 определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила правой руки.
определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила правой руки.
Модуль силы Ампера можно найти по формуле:
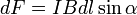 ,
,
где 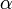 — угол между векторами магнитной индукции и тока.
— угол между векторами магнитной индукции и тока.
Сила 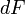 максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции (
максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции (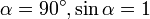 ):
):
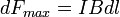 .
.
]Два параллельных проводника
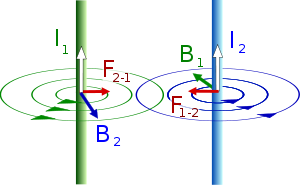
Два бесконечных параллельных проводника в вакууме
Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии  друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи
друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи 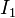 и
и 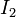 . Требуется найти силу, действующую на единицу длины проводника.
. Требуется найти силу, действующую на единицу длины проводника.
Бесконечный проводник с током 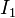 в точке на расстоянии
в точке на расстоянии  создаёт магнитное поле с индукцией:
создаёт магнитное поле с индукцией:
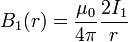 (по закону Био — Савара — Лапласа).
(по закону Био — Савара — Лапласа).
Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:
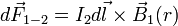
По правилу буравчика, 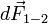 направлена в сторону первого проводника (аналогично и для
направлена в сторону первого проводника (аналогично и для 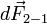 , а значит, проводники притягиваются).
, а значит, проводники притягиваются).
Модуль данной силы ( — расстояние между проводниками):
— расстояние между проводниками):
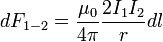
Интегрируем, учитывая только проводник единичной длины (пределы 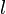 от 0 до 1):
от 0 до 1):
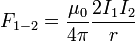
 2015-05-14
2015-05-14 18021
18021
