Лабораторная работа №2-3
Определение горизонтальной составляющей индукции магнитного поля Земли
Цель работы:
Изучить закон Био-Савара-Лапласа и определить горизонтальную составляющую индукции магнитного поля Земли.
Приборы и принадлежности:
Регулируемый источник постоянного тока с коммутатором, тангенс-гальванометр и соединительные провода.
1. Соберите электрическую цепь согласно рис.
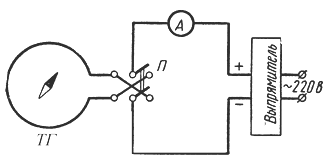
Рис. Схема экспериментальной установки
2. Поворачивая тангенс-гальванометр вокруг вертикальной оси, установите плоскость катушки тангенс-гальванометра в плоскости магнитного меридиана, т. е. добейтесь того, чтобы витки и продольная ось магнитной стрелки находились в одной вертикальной плоскости.
3. Включите источник питания и установите в цепи величину тока, при которой магнитная стрелка компаса отклонится на угол 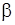 , равный 45º от первоначального положения. Запишите величину тока.
, равный 45º от первоначального положения. Запишите величину тока.
4. Не изменяя величины тока, с помощью коммутатора измените направление тока в витках на противоположное и произведите отсчет угла отклонения 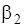 . При этом стрелка компаса отклонится в сторону, противоположную отклонению при первом измерении. Найдите среднее значение
. При этом стрелка компаса отклонится в сторону, противоположную отклонению при первом измерении. Найдите среднее значение 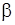 .
.
5. Проведите измерение при других значениях тока, после чего отключите источник питания от сети.
6. Средний радиус R=0,2м витков катушки и число витков N =56.
Для каждой пары значений I и 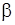 вычислите
вычислите 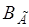 по формуле
по формуле 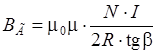 и найдите ее среднее значение.
и найдите ее среднее значение.
7. Рассчитайте погрешность измерений.
Результаты измерений и вычислений занесите в таблицу 1.
Табл. 1
| № п/п | 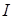 , А , А | 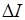 , А , А | 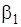 , о , о | 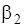 , о , о | 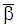 , о , о | 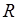 , м , м | 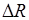 , м , м | 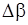 , о , о | 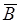 , Тл , Тл | 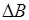 , Тл , Тл |
| 0,2 | 0,2 | 8,82*10-4 | ||||||||
| 0,2 | 0,2 | 8,82*10-4 | 0,0098 | |||||||
| 0,2 | 0,2 | 8,82*10-4 | 0,0096 |
8. Окончательный ответ представить в виде 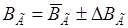 .
.
BA=8,82*10-4 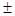 0;
0;
BA=8,82*10-4 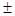 0,0098;
0,0098;
BA=8,82*10-4 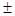 0,0096.
0,0096.
Вопросы для самоконтроля
1. Закон Био-Савара-Лапласа. Применение закона Био-Савара-Лапласа к расчету поля прямого тока.
2. Индукция магнитного поля.
3. Закон Ампера. Применение закона.
Ответы:
Закон Био́-Савара-Лапла́са - физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).
Закон Био-Савара-Лапласа играет в магнитостатике ту же роль, что и закон Кулона в электростатике. Закон Био-Савара-Лапласа можно считать главным законом магнитостатики, получая из него остальные ее результаты.
В современной формулировке закон Био-Савара-Лапласа чаще рассматривают как следствие двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля, т.е. в современной формулировке уравнения Максвелла выступают как более фундаментальные (прежде всего хотя бы потому, что формулу Био-Савара-Лапласа нельзя просто обобщить на общий случай полей, зависящих от времени).
Для тока текущего по контуру (тонкому проводнику)
Пусть постоянный ток течёт по контуру (проводнику), находящемуся в вакууме, — точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)
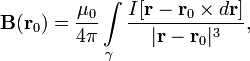
где квадратными скобками обозначено векторное произведение, r - положение точек контура, dr - вектор элемента контура, вдоль которого идет проводник (ток течет вдоль него); - константа (магнитная проницаемость вакуума).
Если же взять за точку отсчёта точку, в которой нужно найти вектор магнитной индукции, то формула немного упрощается:
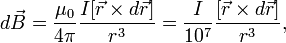
где 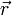 - вектор описывающий кривую проводника с током
- вектор описывающий кривую проводника с током 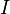 ,
,  - модуль
- модуль 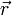 ,
, 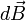 - вектор магнитной индукции, создаваемый элементом проводника
- вектор магнитной индукции, создаваемый элементом проводника 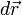 .
.
Направление 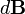 перпендикулярно плоскости, в которой лежат вектора
перпендикулярно плоскости, в которой лежат вектора 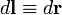 и
и 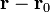 . Направление вектора магнитной индукции может быть найдено по правилу правого винта: направление вращения головки винта дает направление
. Направление вектора магнитной индукции может быть найдено по правилу правого винта: направление вращения головки винта дает направление 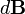 , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора
, если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора 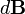 определяется выражением:
определяется выражением:
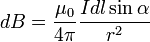
Векторный потенциал даётся интегралом (в системе СИ)
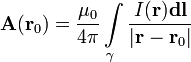
Для распределенных токов
Для случая, когда источником магнитного поля являются распределенные токи, характеризуемые полем вектора плотности тока j, формула закона Био — Савара принимает вид (в системе СИ):
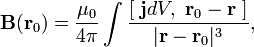
где j = j (r), d V - элемент объема, а интегрирование производится по всему пространству (или по всем его областям, где j ≠ 0), r - соответствует текущей точке при интегрировании (положению элемента d V).
Векторный потенциал:
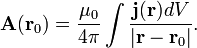
 2015-05-14
2015-05-14 2104
2104