Здесь используется формула рабочего листа МАКС (MAX), которая возвращает максимальное значение среди ее аргументов. Функция МИН (MIN)возвращает минимальное значение среди ее аргументов.
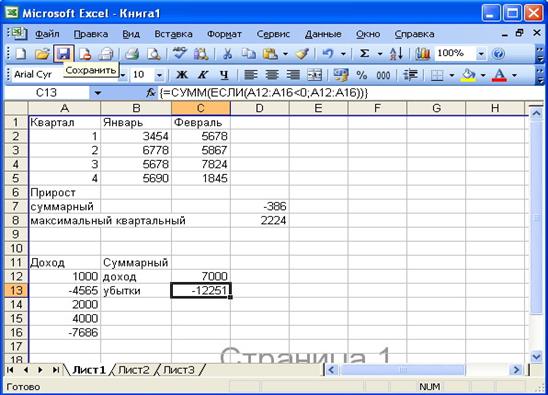
Рис. 3.9. Исключение промежуточных формул
В случае если среди данных имеются как положительные, так и отрицательные значения, формулы массивов позволяют обработать только положительные или отрицательные данные без предварительной их сортировки или фильтрации. Например, пусть в диапазон А12:А16 введены как доходы, так и убытки за отчетный период. Тогда, для того чтобы найти:
□ суммарный доход, достаточно ввести в ячейку С12 формулу массивов:
{=СУММ(ЕСЛИ(А12:А16>0;А12:А16))}
□ суммарный убыток, достаточно ввести в ячейку С13 формулу массивов:
{=СУММ(ЕСЛИ(А12:А16<0;А12:А16))}
Задания
Вариант 1
1. Решить системы линейных уравнений АХ = В, А3Х = В и вычислить значение квадратичной формы 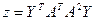 , где
, где
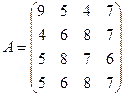 ,
, 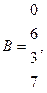
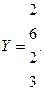
2. Вычислить
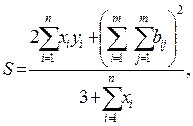
где х, у — векторы из n компонентов, b — матрица размерности m×m, причем n = 4, m = 2 и
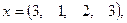
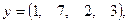
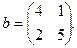
Вариант 2
1. Решить системы линейных уравнений АХ = В, А2АTХ = В и вычислить значение квадратичной формы 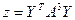 , где
, где
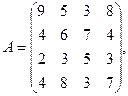
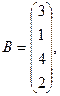
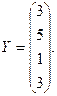
2. Вычислить
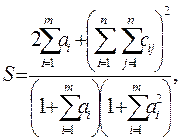
где 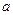 — вектор из m компонентов, с — матрица размерности n×n, причем n = 3, m = 4 и
— вектор из m компонентов, с — матрица размерности n×n, причем n = 3, m = 4 и
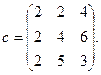
Вариант 3
1. Решить системы линейных уравнений АХ = В, ААTАХ = В и вычислить значение квадратичной формы 
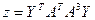 , где
, где
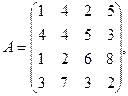
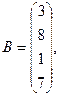
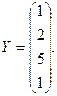
2. Вычислить
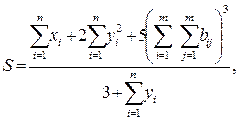
где x, y — векторы из n компонентов, b — матрица размерности m×m, причем n = 4, m = 2 и
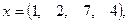
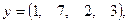
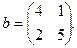
Вариант 4
1. Решить системы линейных уравнений АХ = B, А2АTАХ = В и вычислить значение квадратичной формы 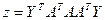 , где
, где
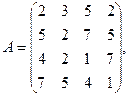
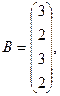
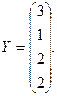
2. Вычислить
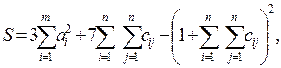
где 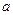 — вектор из m компонентов, с — матрица размерности n×n, причем n = 3, m = 4 и
— вектор из m компонентов, с — матрица размерности n×n, причем n = 3, m = 4 и
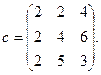
Вариант 5
1. Решить системы линейных уравнений АХ = В, ААTА2Х = B и вычислить значение квадратичной формы 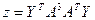 , где
, где
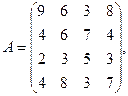
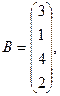
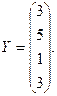
2. Вычислить
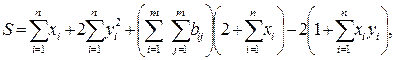
где х, у — векторы из n компонентов, b — матрица размерности m×m, причем n = 4, m = 2 и
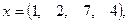
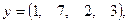
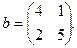
Вариант 6
1. Решить системы линейных уравнений АХ = В, А3АTХ = В и вычислить значение квадратичной формы 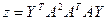 , где
, где
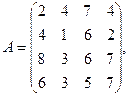
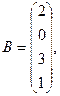
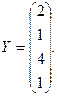
2. Вычислить
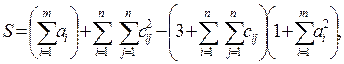
где 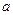 — вектор из m компонентов, с — матрица размерности n×n, причем n = 3, m = 4 и
— вектор из m компонентов, с — матрица размерности n×n, причем n = 3, m = 4 и
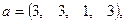
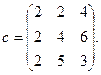
Вариант 7
1. Решить системы линейных уравнений АХ = В, АTА3Х = В и вычислить значение квадратичной формы 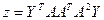 , где
, где
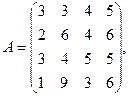
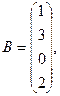
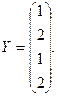
2. Вычислить
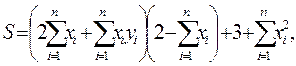
где х, y — векторы из n компонентов, причем n = 4 и
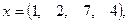
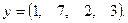
Вариант 8
1. Решить системы линейных уравнений АХ = В, ААTА2Х = В и вычислить значение квадратичной формы 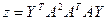 , где
, где
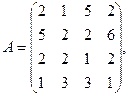
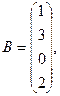
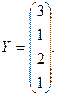
2. Вычислить
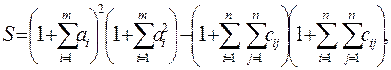
где 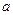 — вектор из m компонентов, с — матрица размерности n×n, причем n = 2, m = 4 и
— вектор из m компонентов, с — матрица размерности n×n, причем n = 2, m = 4 и
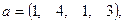
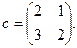
Вариант 9
1. Решить системы линейных уравнений АХ = В, АTААTX = В и вычислить значение квадратичной формы 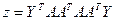 , где
, где
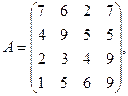
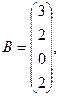
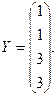
2. Вычислить
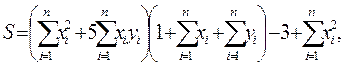
где x, y – векторы из n компонентов, причем n = 4 и
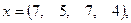
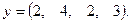
Вариант 10
1. Решить системы линейных уравнений АХ = В, A2ATAX = B и вычислить значение квадратичной формы 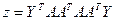 , где
, где
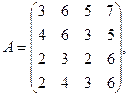
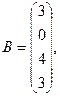
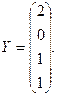
2. Вычислить
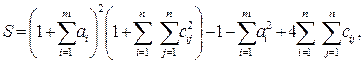
где 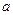 - вектор из m компонентов, с –матрица размерности n×n, причем n = 3, m = 4 и
- вектор из m компонентов, с –матрица размерности n×n, причем n = 3, m = 4 и
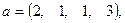
 2015-05-14
2015-05-14 679
679







