Магнитостатическая энергия

Пусть имеется несколько постоянных магнитов, расположенных так, что расстояния между ними велики по сравнению с их размерами, тогда конфигурация поля будет похожа на картину поля, создаваемую электрическими диполями. Предположим, что эти магнитные диполи образованы фиктивными магнитными зарядами ±m_i, (математическая абстракция), расстояния между которыми l_i. Обозначим магнитные заряды полюсов через m₁, m₂, … m_i, а магнитный потенциал в точках расположения полюсов через Ф₁, Ф₂, Ф… Ф_i, тогда потенциальная энергия будет иметь вид: 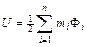. Здесь потенциал Ф_i, создается всеми зарядами, кроме i – го. Из электростатики известно, что 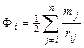. Здесь r_ij – расстояние между i – тым и j – тым магнитными зарядами.

Энергия U называется магнитостатической энергией. Если магнитные заряды распределены в пространстве с плотностью r, то магнитостатическая энергия может быть записана в виде: 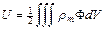, где магнитный потенциал определяется как 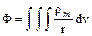, где r – расстояние между рассматриваемой точкой и местом расположения заряда rdv.

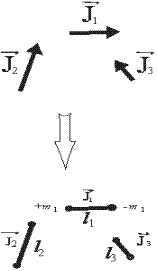Рис. 2. Замена магнитных моментов системой диполей.

Теперь выразим магнитостатическую энергию через намагниченность и поле, создаваемое этой намагниченностью (размагничивающее поле). Пусть «длина» i – того диполя l_i, а заряды на его концах ±m_i. Тогда по аналогии с электрическим диполем его магнитный момент: J_i=m_i l_i. Пусть так же компонента магнитного поля вдоль J_i будет H_||, тогда DF=F₊-F_-= - H_|| l_i, откуда получаем:

m⁺_iF₊-m^-_iF_-= - (m_i/ l_i.)(H_|| l_i) = - m _i H _i.

Перепишем выражение для магнитостатической энергии в другом виде:

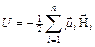
Необходимо иметь ввиду, что H _i – поле, созданное всеми (кроме i–того) диполями в месте расположения i–того диполя. Если намагниченность и поле H _m заданы в виде функции координат, то магнитостатическая энергия определяется интегрированием по объему плотности магнитостатической энергии

E_m= - (1/2) J _s(x) H_m(x): Здесь V – объем магнетика