Метод порошковых фигур Акулова – Биттера (магнитной суспензии) был применен при первых наблюдениях ДС [1], которые подтвердили её существование и состоит в нанесении на хорошо полированную поверхность магнитного материала магнитной суспензии (взвешенные в жидкости однодоменные частицы магнетита Fe3O4). На частицы действует сила F~m(dH/dx). Эти частицы притягиваются в область доменных границ, поскольку наибольший градиент поля вблизи края доменов. При этом, как правило, прорисовываются доменные границы. Применяется метод темного поля (наблюдаются светлые границы на темном фоне) и метод светлого поля (наблюдаются темные границы на светлом фоне).
Важным этапом в аттестации ДС является расшифровка картин. Расшифровка предполагает – составление схемы расположения доменов, ориентации доменных границ и намагниченности в доменах. Для этого необходимо знать кристаллографию, изучить движение ДГ в поле, и использовать зонды и царапины для определения направления намагниченности J. Кроме того необходимо знать принципы формирования ДС, и известные теоретические модели.
Недостатком этого метода является инерционность выявления ДС при ее изменении и ограниченность температурного интервала измерений.
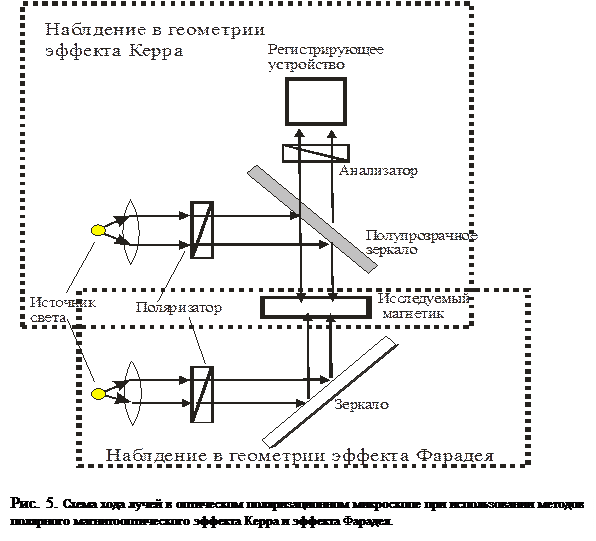
Метод магнитооптического эффекта Фарадея, Керра (полярный, меридиональный). Эффект Фарадея – явление вращения плоскости поляризации при прохождении света через прозрачный магнетик на угол jф =kL, где k – постоянная Фарадея, L – толщина кристалла.Оптический контраст разнополярных доменов создается благодаря различному знаку угла фарадеевского вращения в них. Пучки света, проходящие через разнополярные домены, меняют свою интенсивность при прохождении через анализатор (рис. 5).
При наблюдении методом полярного магнитооптического эффекта Керра контраст доменов создается так же благодаря вращению плоскости поляризации в них при падении плоскополяризованной световой волны на металлическую отражающую поверхность образца и последующем ее отражении. Схема хода лучей в геометрии Фарадея и Керра показана на рис. 5.
Картины ДС прозрачных пластин ферритов гранатов получаются цветными, причем, благодаря дисперсии фарадеевского вращения, домены, имеющие различную нормальную компоненту намагниченности, окрашены в различные цвета. Это позволяет в процессе намагничивания проводить идентификацию различных фаз, в которых J s имеет различную нормальную компоненту.
 2015-05-14
2015-05-14 2219
2219
