п- го порядка при помощи MathCAD
Методика решения задачи Коши для дифференциального уравнения порядка 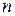 является развитием методики, которая применяется для решения задачи Коши для дифференциального уравнения первого порядка – с использованием встроенной функции rkfixed. Различие состоит в следующем.
является развитием методики, которая применяется для решения задачи Коши для дифференциального уравнения первого порядка – с использованием встроенной функции rkfixed. Различие состоит в следующем.
Вектор начальных значений y состоит из 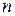 элементов, определяющих начальные условия для искомой функции и ее производных
элементов, определяющих начальные условия для искомой функции и ее производных 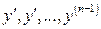 .
.
Функция D является вектором, содержащим 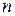 элементов:
элементов:
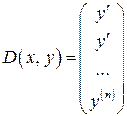 .
.
Матрица, получаемая в результате решения, содержит 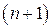 столбцов: первый – значения
столбцов: первый – значения 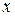 , оставшиеся столбцы – значения
, оставшиеся столбцы – значения 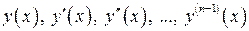 соответственно.
соответственно.
Для того чтобы решить задачу Коши для дифференциального уравнения п-го порядка при помощи MathCAD, необходимо:
1. Задать вектор начальных условий 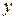 в виде матрицы-столбца.
в виде матрицы-столбца.
2. Определить функцию 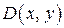 в виде матрицы-столбца, в котором последний элемент – старшая производная, выраженная из исходного дифференциального уравнения.
в виде матрицы-столбца, в котором последний элемент – старшая производная, выраженная из исходного дифференциального уравнения.
3. Задать количество точек, в которых будем искать решение.
4. Задать массив численного решения поставленной задачи, используя встроенную функцию rkfixed.
5. Вывести массив искомого решения и построить его график.
Пример. Найти решение уравнения 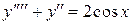 с начальными условиями
с начальными условиями 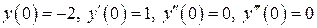 в ста промежуточных точках на отрезке
в ста промежуточных точках на отрезке 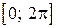 .
.
 2015-05-14
2015-05-14 255
255








