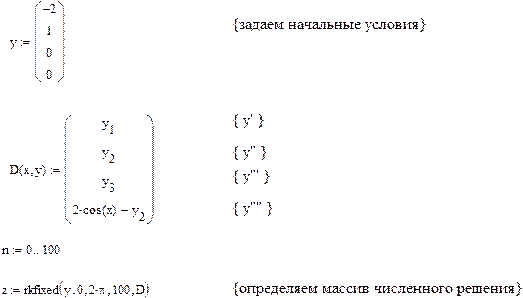
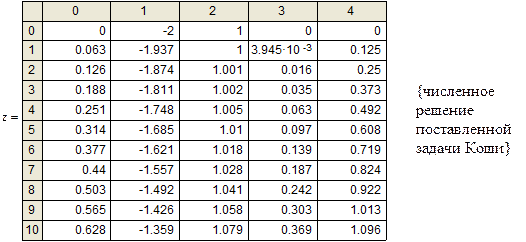
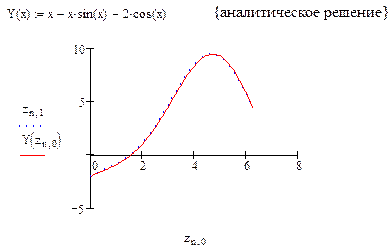
Сравним полученное численное решение с аналитическим, построив их графики в одной системе координат.
Задания для самостоятельного решения
Решить задачу Коши для дифференциального уравнения порядка  на отрезке
на отрезке 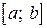 . Решение произвести двумя способами: численно и аналитически. Построить графики полученных решений в ста промежуточных точках.
. Решение произвести двумя способами: численно и аналитически. Построить графики полученных решений в ста промежуточных точках.
| 1. | а) 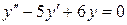 , , 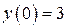 , , 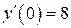 , , 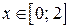 ;
б) ;
б) 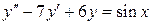 , , 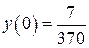 , , 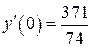 , , 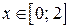 . .
|
| 2. | а) 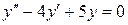 , , 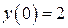 , , 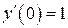 , , 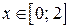 ;
б) ;
б) 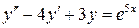 , , 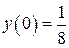 , , 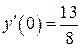 , , 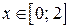 . .
|
| 3. | а) 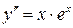 , , 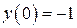 , , 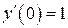 , , 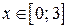 ;
б) ;
б) 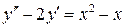 , , 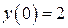 , , 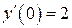 , , 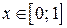 . .
|
| 4. | а) 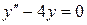 , , 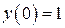 , , 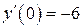 , , 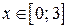 ;
б) ;
б) 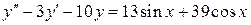 , , 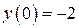 , , 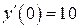 , , 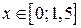 . .
|
| 5. | а) 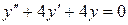 , , 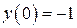 , , 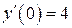 , , 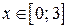 ;
б) ;
б) 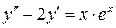 , , 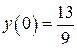 , , 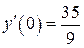 , , 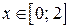 . .
|
| 6. | а) 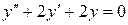 , , 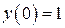 , , 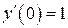 , , 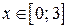 ;
б) ;
б) 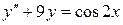 , , 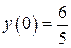 , , 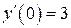 , , 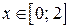 . .
|
| 7. | а) 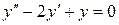 , , 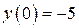 , , 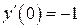 , , 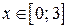 ;
б) ;
б) 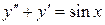 , , 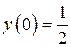 , , 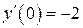 , , 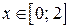 . .
|
| 8. | а) 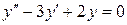 , , 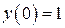 , , 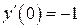 , , 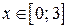 ;
б) ;
б) 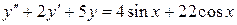 , , 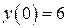 , , 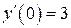 , , 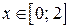 . .
|
| 9. | а) 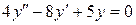 , , 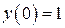 , , 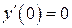 , , 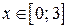 ;
б) ;
б) 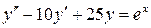 , , 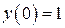 , , 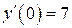 , , 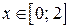 . .
|
| 10. | а) 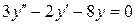 , , 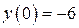 , , 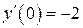 , , 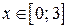 ;
б) ;
б) 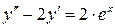 , , 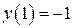 , , 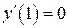 , , 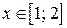 . .
|
| 11. | а) 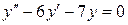 , , 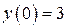 , , 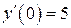 , , 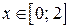 ;
б) ;
б) 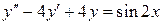 , , 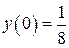 , , 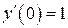 , , 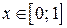 . .
|
| 12. | а) 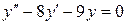 , , 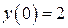 , , 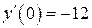 , , 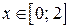 ;
б) ;
б) 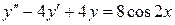 , , 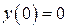 , , 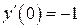 , , 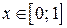 . .
|
| 13. | а) 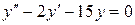 , , 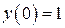 , , 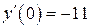 , , 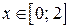 ;
б) ;
б) 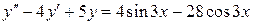 , , 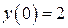 , , 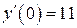 , , 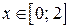 . .
|
| 14. | а) 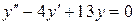 , , 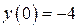 , , 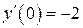 , , 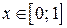 ;
б) ;
б) 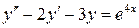 , , 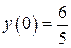 , , 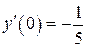 , , 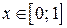 . .
|
| 15. | а) 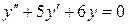 , , 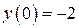 , , 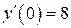 , , 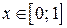 ;
б) ;
б) 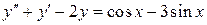 , , 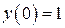 , , 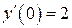 , , 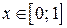 . .
|
| 16. | а) 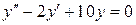 , , 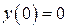 , , 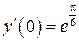 , , 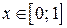 ;
б) ;
б) 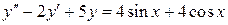 , , 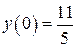 , , 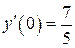 , , 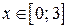 . .
|
| 17. | а) 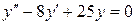 , , 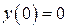 , , 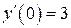 , , 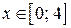 ;
б) ;
б) 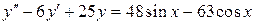 , , 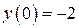 , , 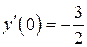 , , 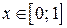 . .
|
| 18. | а) 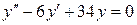 , , 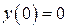 , , 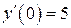 , , 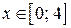 ;
б) ;
б) 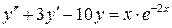 , , 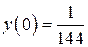 , , 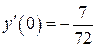 , , 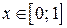 . .
|
| 19. | а) 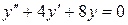 , , 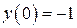 , , 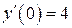 , , 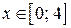 ;
б) ;
б) 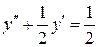 , , 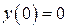 , , 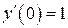 , , 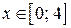 . .
|
| 20. | а) 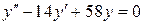 , , 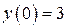 , , 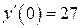 , , 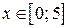 ;
б) ;
б) 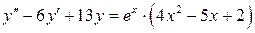 , , 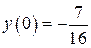 , , 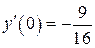 , , 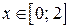 . .
|
 2015-05-14
2015-05-14 201
201







