Условный экстремум

Нередко при отыскании экстремума функции многих переменных аргументы функции связаны между собой одним или несколькими уравнениями, называемыми уравнениями связи. Число таких уравнений, естественно, должно быть меньше числа переменных величин, в противном случае переменные величины могут превратиться (при решении системы) в постоянные величины.

В этом случае, как правило, говорят об условном экстремуме. В отличие от обычного экстремума здесь речь идет о точках, координаты которых удовлетворяют уравнению связи. Предположим, что задана функция у = ƒ (х, у) и уравнение связи у = φ (х), представляемое линией L на плоскости 0ХУ. При этом задача отыскания условий экстремума функции Z = ƒ (х, у) будет состоять в том, чтобы на линии L найти такие точки, в которых значения функции будут наибольшими или наименьшими по сравнению со значениями ее в достаточно близких точках линии L.

Рассмотрим задачу на отыскание условий экстремума функции для того случая, когда задана функция двух переменных Z = ƒ (х, у), а уравнение связи имеет вид φ (х, у) = 0.

Если уравнение связи разрешимо относительно у, т.е. из него можно явно выразить у через х: у = ψ (x), то, делая подстановку в выражение функции Z = ƒ (х, у), получим функцию одной переменной:

Z = ƒ [x, ψ (x)] = F (x).

В случае, когда из уравнения связи не удается выразить одну переменную через другую, пользуются так называемым методом неопределенных множителей Лагранжа. Чтобы найти точки, которые могут быть точками условного экстремума функции Z = ƒ(х, у) при уравнении связи φ(х, у) = 0, нужно образовать вспомогательную функцию (ее часть называют функцией Лагранжа).

Ф (х, у) = ƒ (х, у) + λφ (х, у),

где λ - некоторая постоянная.

Затем, необходимо составить уравнение для отыскания точек экстремума. Очевидно, что таких уравнения должно быть три по числу неизвестных: х, у, λ.

Находим частные производные функции Ф (х, у) и используя необходимые условия существования экстремума функции получим эти три уравнения:

ƒ'x (x, y) + λφ'x (x, y) = 0

ƒ'y (x, y) + λφ'y (x, y) = 0

φ (x, y) = 0

Пример 1. Найти экстремум функции

Z = x + y

при условии, что

.

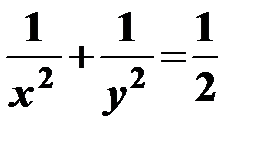Решение:

а). Составляем функцию Лагранжа

Ф (х, у) = х + у + λ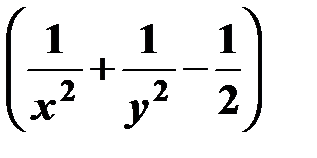

б). Находим частные производные первого порядка

;

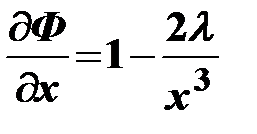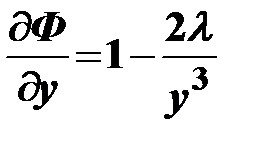
с). Используя необходимые условия существования экстремума функции Ф (х, у) и уравнение связи, получаем систему:

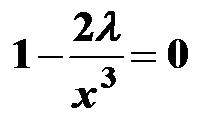
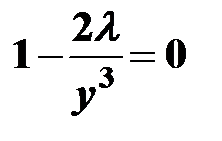
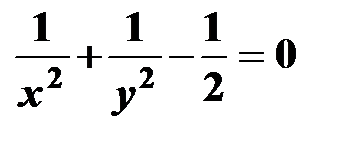
д). Далее решая последнюю систему и используя условия экстремума, получаем две критические точки:

Р ₂ (-2, -2); Р ₂ (2, 2).

В первом случае функция имеет значения - 4, а во втором +4. В точке Р₂ функция Z имеет максимум, а в точке Р₂ - минимум.

Пример 2. Требуется найти экстремум функции

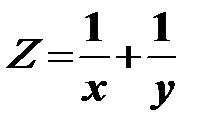
при условиях, что

х + у = 2.

Решение. Также составляем функцию Лагранжа:

Ф (х, у) =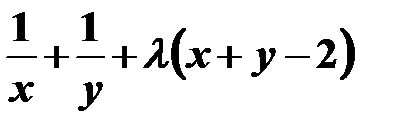

Находим частные производные первого порядка функции Лангранжа:

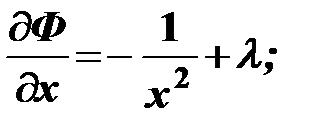
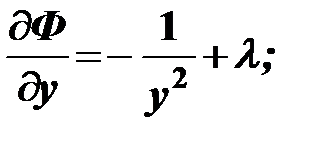
Составляем систему уравнений:

.

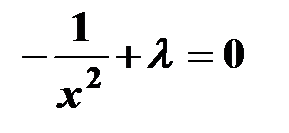
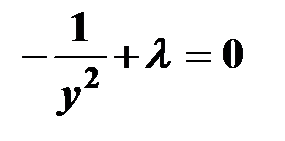х + у - 2 = 0

Можно показать, что в точке (1,1) данная функция Z имеет минимум, равное 2.

Примечание. Данный пример в виду его простоты можно решить и без использования функции Лагранжа.