C) Форма контроля

· Защита лабораторных работ СРС 1. Устный опрос работа сдаются в виде отчета.

D) Оценочный балл выполнения задания – 20 балл.

E) Список рекомендуемой литературы

1. Р.У. Рахметова Эконометрика. Алматы. 2009. 226с.

2. И.И. Елисеева. Эконометрика. – М.: «Финансы и статистика»,2005.

3. Сапарбаев А.Ж., Макулова А.Т. Эконометрика. Алматы. Бастау.2007. -214с.

4. Мухамедиев Б.М. Эконометрика и эконометрические прогнозирование. Алматы: Қазақ университеті. 2007.-250с.

5. Р.У. Рахметова Краткий курс по эконометрике. Учебное пособие. Алматы. 2004. -78с.

6. Джонстон Дж. Эконометрические методы. Пер. с англ. – М.: Статистика, 1980 – 444 с.

7. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учебник. – М.: Дело, 2001. – 400 с.

8. Практикум по эконометрике: Учебное. пособие / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.

9. А.Ю. Козлов, В.Ф. Шишов Пакет анализа MS Excel в экономическо-статистических расчетов.

10. Электрондық оқулық «Эконометрика» (авторлары: Мухамедиев Б.М., Бордоусов О.В.)- оқыту WEB – экономистер және юристре үшін портал Univer.kz., 2004.

3. Название темы: Множественная регрессия

a) Задания СРСП. По 30 территориям Казахстана имеются данные, представленные в табл. 2.1.

Требуется:

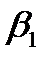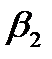1. Построить уравнение множественной регрессии в стандартизированной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с и , пояснить различия между ними.

2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.

3. Рассчитать общий и частные 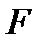-критерии Фишера.

b) Методические рекомендации по выполнению заданий

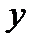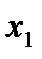1. Линейное уравнение множественной регрессии от и 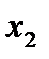имеет вид: 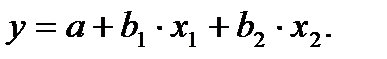Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: .

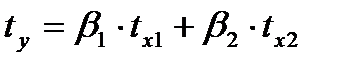Расчет 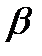-коэффициентов выполним по формулам

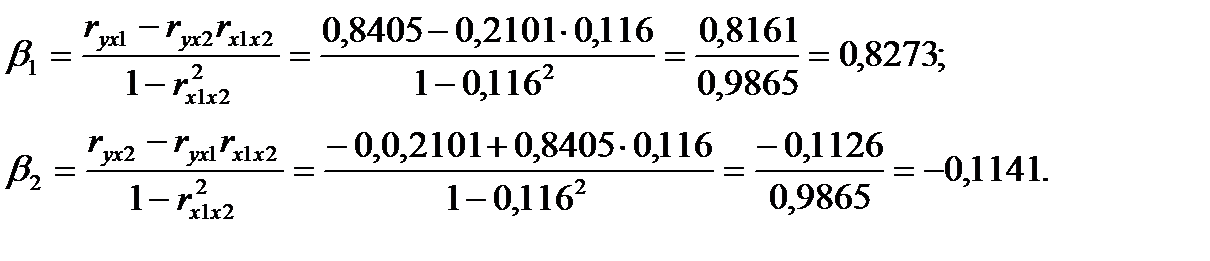Получим уравнение

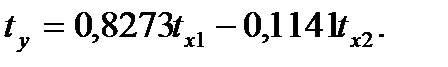
Для построения уравнения в естественной форме рассчитаем 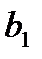и 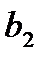используя формулы для перехода от 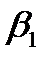к :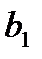

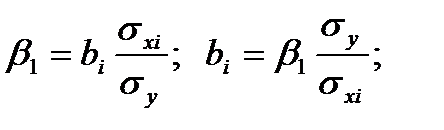
Значение 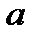определим из соотношения

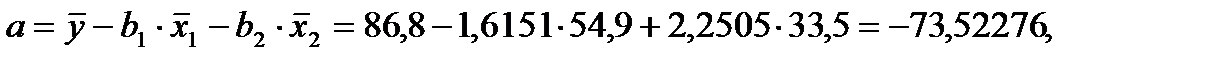
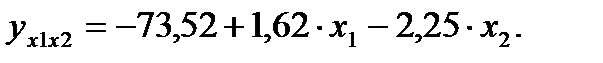
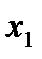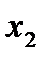Для характеристики относительной силы влияния и на 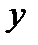рассчитаем средние коэффициенты эластичности:

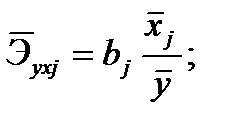
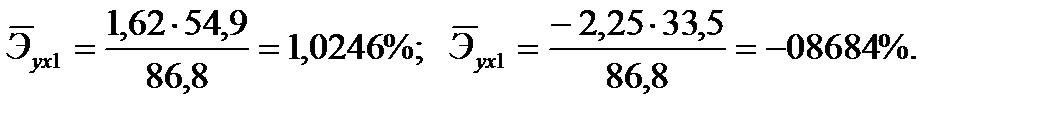
С увеличением средней заработной платы 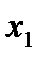на 1% от ее среднего уровня средний душевой доход 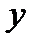возрастает на 1,02% от своего среднего уровня; при повышении среднего возраста безработного 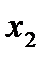на 1%

среднедушевой доход 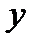снижается на 0,87% от своего среднего уровня. Очевидно, что сила влияния средней заработной платы 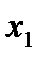на средний душевой доход 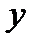оказалась большей, чем сила влияния среднего возраста безработного 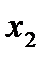. К аналогичным выводам о силе связи приходим при сравнении модулей значени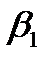й и :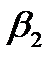

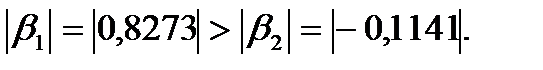
Различия в силе влияния фактора на результат, полученные при сравнени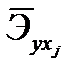и и 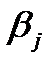, объясняются тем, что коэффициент эластичности исходит из соотношения средних: 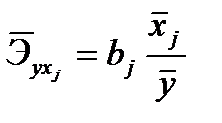, а 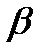-коэффициент – из соотношения средних квадратических отклонений: .

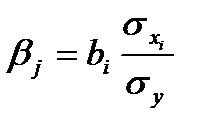2. Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле:

;

;

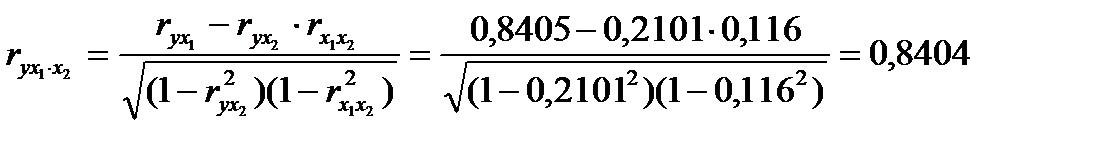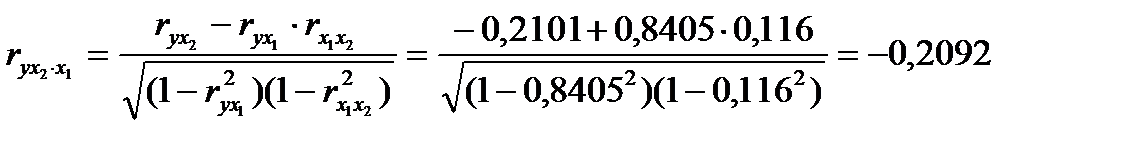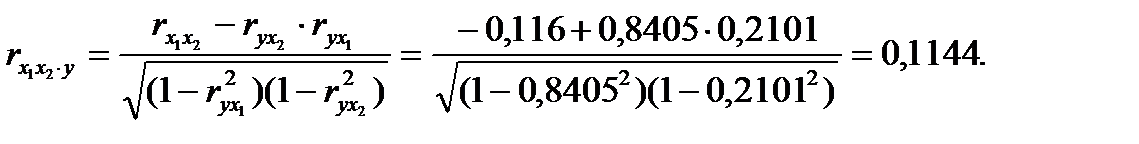
Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи 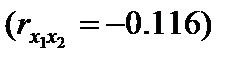коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:

;

.

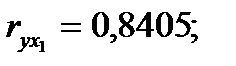
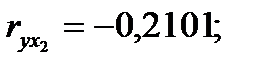
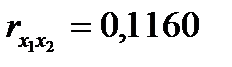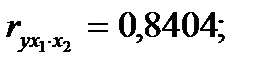
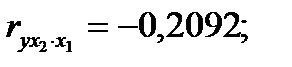
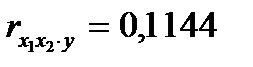Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов 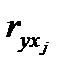и :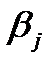

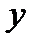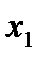Зависимость от и 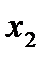характеризуется как тесная, в которой 72% вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28% от общей вариации .

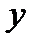3. Общий 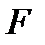-критерий проверяет гипотезу 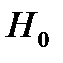о статистической значимости уравнения регрессии и показателя тесноты связи :

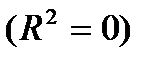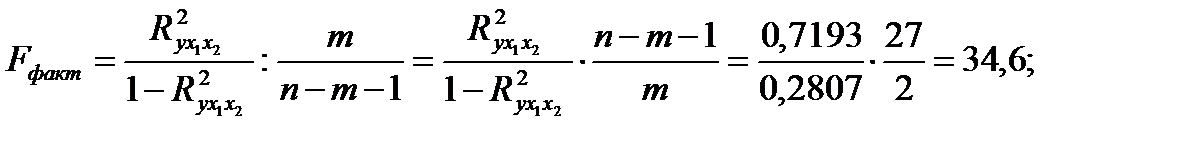
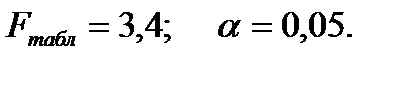
Сравнивая 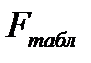и 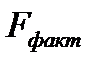, приходим к выводу о необходимости отклонить гипотезу 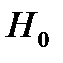, так как 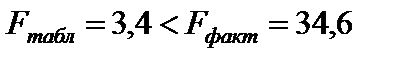c вероятностью 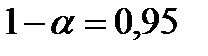делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи 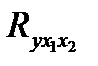, которые сформировались под неслучайным воздействием факторов 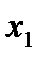и .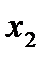

Частные 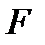-критери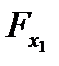и - и 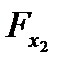оценивают статистическую значимость присутствия факторов 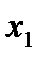и 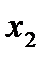в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. 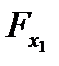оценивает целесообразность включения в уравнение фактора 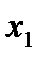после того, как в него был включен фактор 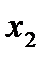. Соответственно 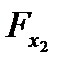указывает на целесообразность включения в модель фактора 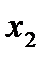после фактора :

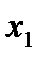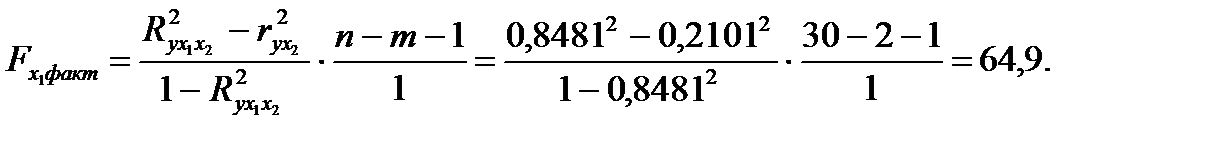
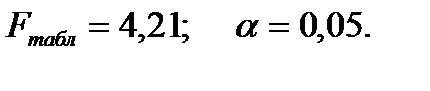
Сравнивая 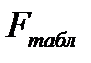и 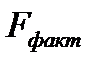, приходим к выводу о целесообразности включения в модель фактора 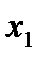после фактора 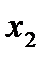, так как 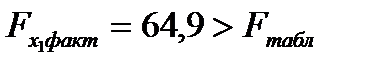. Гипотезу 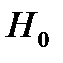о несущественности прироста 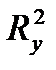за счет включения дополнительного фактора 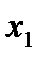отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора 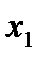после фактора .

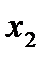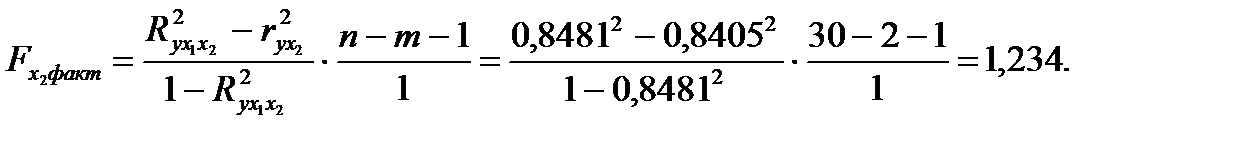
Низкое значение 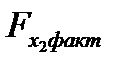(немногим больше 1) свидетельствует о статистической незначимости прироста 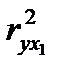за счет включения в модель фактора 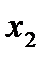после фактора 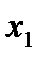. Следовательно, подтверждается нулевая гипотеза 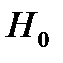о целесообразности включения в модель фактора 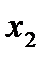(средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор 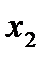(средний возраст безработного).