Ожидаемое значение случайной переменной , её дисперсия и ср. квадратичное отклонение

В эконометрике важную роль играют две колличественные характеристикиеи случайной переменной х: математическое ожидание и дисперсия. Ожидаемое значение Е(х) находится по формуле

Е(х)= m= 1.) 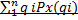для дискретной Х; 2.) 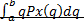для непрерывной х.

Подчеркнем,что Е(х) – это константа, вокруг которой рассеяны возможные значения q случайной переменной х.

Дисперсия Var(x) – это средний квадрат разброса возможных значений случайной переменной х относительно её ожидаемого значения:

Var(x) = 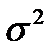= E(x-m)² = 1.) 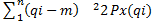; 2.)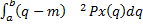

Так что Var(x) – это тоже константа, физическая размерность которой равна квадрату физической размерности значений х. Положительный квадратный корень из дисперсии = 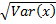именуется средним квадратичным отклонением. Размерности и х совпадают. Константа служит характеристикой неопределенности х. Добавим, что при вычислении Var(x) удобно пользоваться формулой, вытекающей из формулы: 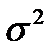= E(x²) – m² .

Из всех вышеперечисленных формул видно,что для отыскания величин m, 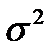нужно знать закон распределения P_x(q) случайной переменной х. Часто это закон неизвестен, и тогда можно оценить характеристики m, 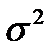по результатам n независимых наблюдений над х.

(х₁,х₂,…,х_n)

В наборе каждая композиция х_i - это случайная переменная с одним и тем же законом распределения Р_х(q), при этом величины х_i являются независимыми. Вот формулы для оценивания m, :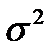

M ≈ = =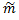

≈ = =

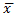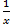
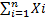
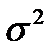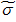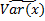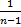
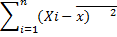
С ростом количества наблюдений n точность приближенных формул возрастает.