Нормальный закон распределения как характеристика случайной переменной

Непрерывная случайная величина Х называется распределенной по нормальному закону с параметрами μ и σ, если ее плотность распределения есть

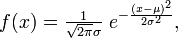
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Если случайные величины X1 и X2 независимы и имеют нормальное распределение с математическими ожиданиями μ1 и μ2 и дисперсиям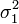и и 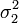соответственно, то X1 + X2 также имеет нормальное распределение с математическим ожиданием μ1 + μ2 и дисперсией .

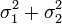Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

· отклонение при стрельбе

· погрешности измерений

· рост живых организмов