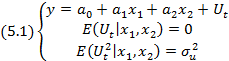
y – эндогенная переменная
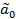 ,
, 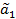 ,
, 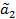 ,
, 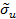 - параметры
- параметры
Эконометрическая инвестиционная модель Самуэльсона-Хикса является частным случаем модели (5.1). Она является моделью парной регрессии, т.к. имеет 2 переменных (а именно: эндогенную 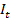 и предопределённую
и предопределённую 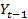 )
)
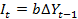
Далеко не всегда удаётся подобрать процедуру, обеспечивающую получение несмещённых и эффективных оценок при большом объёме выборки.
(Напоминаю: оценка параметров закона распределения называется несмещённой, если её математическое ожидание совпадает со значением параметра: 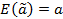 ; эффективной среди всех несмещённых оценок называется та, которая имеет минимальную дисперсию (σ→min)(выбирается та процедура, которая даёт минимальный разброс значения оценки)).
; эффективной среди всех несмещённых оценок называется та, которая имеет минимальную дисперсию (σ→min)(выбирается та процедура, которая даёт минимальный разброс значения оценки)).
Поэтому вводится понятие асимптотически несмещённых и асимптотически эффективных оценок, для которых свойства несмещённости и эффективности достигаются при неограниченном увеличении объёма выборки. Однако и такие оценки получаются не всегда. Удовлетворительными будут оценки, обладающие свойством несмещённости при больших объёмах выборки. Такие оценки называются состоятельными.
Одним из методов, позволяющих получить состоятельные оценки, является метод наименьших квадратов (МНК) (определён К.Ф. Гауссом (1777-1855))
В качестве критериев используется ∑ квадратов невязок (остатков), разности между абсциссами реальных точек и соответствующих точек на прямой.
Решение данных задач получило название регрессионного анализа
Рассмотрим механизм применения МНК на основе применения идентификации модели в виде линейной модели парной регрессии.
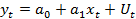 (5.8)
(5.8)
Для решения задач имеем некий набор наблюдений переменных y и x размерностью n.
Согласно МНК, необходимо найти такие значения параметров оценки модели (5.8), которые соответствуют минимуму суммы квадратов остатка.
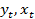 - переменные
- переменные
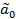 ,
, 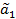 ,
, 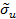 – параметры
– параметры
Из (5.8) следует, что необходимо найти минимум следующей функции (Q):
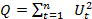 =
= 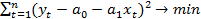 (5.9)
(5.9)
Для нахождения параметров функции (5.9), соответствующих её минимуму, необходимо вычислить производную функции по этим параметрам, приравнять к нулю и решить полученное уравнение относительно параметров.
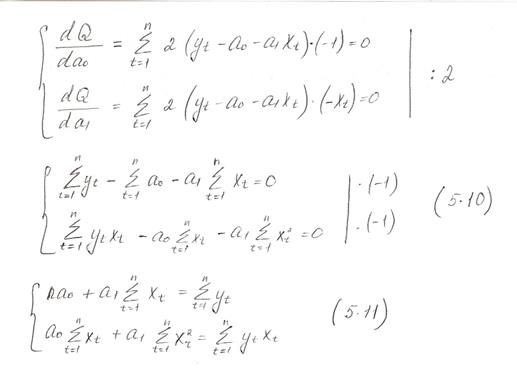
(5.11) - Система нормальных уравнений для определения оценок параметров модели (5.8).
Убедимся, что решения системы уравнения (5.11) соответствуют линейному уравнению (5.9). Для этого вторые производные функции (5.9) должны быть положительными
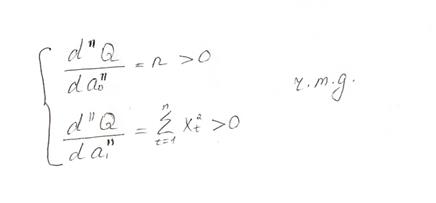
Следовательно, решение системы (5.11) соответствует минимуму функции (5.9).
Систему уравнений (5.11) можно решить методом исключения переменных. Для этого достаточно выразить параметр 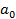 через
через 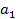 , подставив его во второе уравнение системы, откуда получен
, подставив его во второе уравнение системы, откуда получен 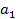 , затем уже
, затем уже 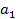 подставить в первое уравнение.
подставить в первое уравнение.
В итоге:
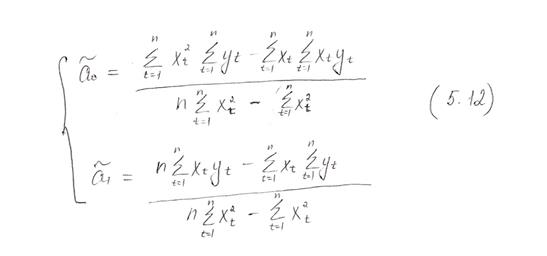
Выражение (5.12) позволяет по известным значениям наблюдений переменных x и y вычислить оценки параметров модели парной регрессии.
 2015-05-18
2015-05-18 824
824

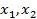 -
- 






