Методы оценивания СОУ. Косвенный МНК. Двухшаговый МНК. Применимость и свойства оценок

На основе обычного МНК невозможно получить на основе качественных оценок параметров системы одновременных уравнений.

Алгоритм косвенного метода наименьших квадратов:

· Структурная модель преобразовывается в приведенную форму модели. Прим:

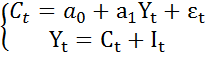
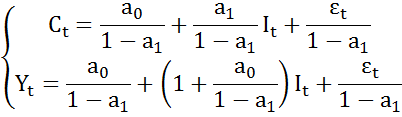
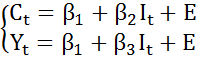
· Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты;

· Коэффициенты приведенной формы модели трансформируются в параметры структурной формы модели.

Недостаток: если уравне­ние сверхидентифицируемо, то один и тот же структурный коэффициент допускает разные выражения че­рез коэфф приведенной формы.

Двухшаговый МНК состоит в том, что оценивают параметры отдельного уравнения системы, а не рассматривают сис-му в целом.

Алгоритм двухшагового метода наименьших квадратов:

Обозначим:

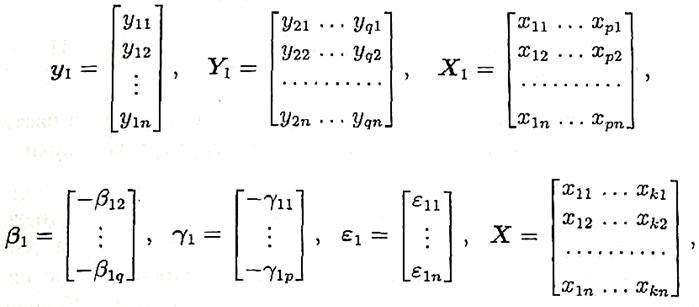
и перепишем в виде: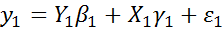

1) проводится регрессия каждого столбца матрицы 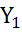на все экзогенные переменные, т.е. рассматривается регрессия

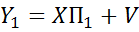, где П₁ матрица коэфф приведенной формы;

2) строится прогнозное значени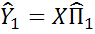е , где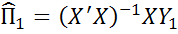

3) осуществляется регрессия 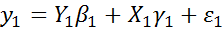с заменой в правой части 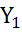на 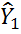т.е. строятся МНК-оценки структурных параме­тров 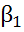и 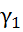регрессии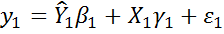

Применение ДМНК будет эффективным лишь в том случае, когда коэффициент детерминации R2 для приведенных уравнений, построенных на первом этапе, будет достаточно высоким. В этом случае инструментальные переменныев очень малой степени коррелируют со случайным отклонением и будут близки к истинному значению (r) заменяемых переменных.