Ряд 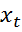 называют строго стационарным (в узком смысле), если совместное распределениеm наблюдений
называют строго стационарным (в узком смысле), если совместное распределениеm наблюдений 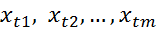 не зависит от сдвига по времени, т.е совпадает с распределением
не зависит от сдвига по времени, т.е совпадает с распределением 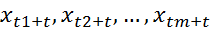 . Слабая стационарность (в широком смысле) состоит в том, что дисперсия и ковариация
. Слабая стационарность (в широком смысле) состоит в том, что дисперсия и ковариация 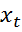 не зависит от момента времени:
не зависит от момента времени: 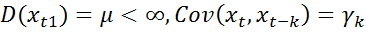 .
.
Значения уровней временных рядов экономических показателей могут содержать следующие компоненты:- тренд 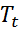 (изменение, определяющее общее направление развития, основную тенденцию временного ряда);- сезонную компоненту
(изменение, определяющее общее направление развития, основную тенденцию временного ряда);- сезонную компоненту 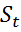 ;- циклическую компоненту
;- циклическую компоненту 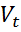 ;- случайную составляющую
;- случайную составляющую 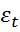 .
.
Анализ временного ряда надо начинать с построения графика исследуемого показателя. По графику можно сделать предположение о наличии тренда и колебаний. Если амплитуда колебаний относительного среднего значения не меняется, то используют аддитивную модель; если же амплитуда возрастает (убывает), то используют мультипликативную модель.
Если присутствие тренда во временном ряду визуально прослеживается нечетко, то проводят статистическую проверку гипотезы о существовании тенденции, например, с помощью метода Фостера-Стюарта:
1) Каждый уровень ряда 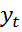 сравнивается со всеми предшествующими, вычисляются вспомогательные характеристики
сравнивается со всеми предшествующими, вычисляются вспомогательные характеристики 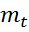 и
и 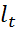 :
:
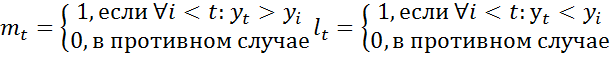
Т.е. 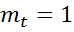 , если
, если 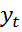 больше всех предшествующих уровней;
больше всех предшествующих уровней; 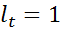 , если
, если 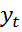 меньше всех предшествующих уровней.
меньше всех предшествующих уровней.
2) Вычисляется 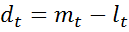 ,
, 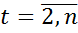 .
.
3) Находится характеристика 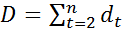 .
.
4) С помощью критерия Стьюдента проверяется гипотеза о том, что можно считать случайной разность 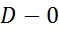 (т.е. ряд можно считать случайным, не содержащим тренд). Для этого определяется
(т.е. ряд можно считать случайным, не содержащим тренд). Для этого определяется 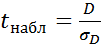 , где
, где 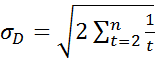 – средняя квадратическая ошибка величины D. Расчетное значение критерия
– средняя квадратическая ошибка величины D. Расчетное значение критерия 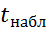 сравнивается с критическим значением
сравнивается с критическим значением 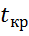 для заданного уровня значимости a и числа степеней свободы
для заданного уровня значимости a и числа степеней свободы 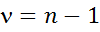 . Если
. Если 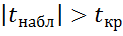 , то гипотеза об отсутствии тренда отвергается.
, то гипотеза об отсутствии тренда отвергается.
При наличии у временного ряда тренда, циклической и сезонной компонент наблюдается корреляция между уровнями временного ряда – автокорреляция. Количественно автокорреляция устанавливается с помощью линейного коэффициента корреляции между уровнями этого ряда и некоторым лагом 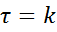 . Величина лага определяет порядок коэффициента корреляции. Коэффициент автокорреляции k-го порядка вычисляется по формуле:
. Величина лага определяет порядок коэффициента корреляции. Коэффициент автокорреляции k-го порядка вычисляется по формуле:
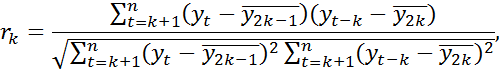
где 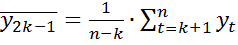 ,
, 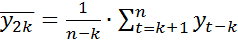 .
.
С увеличением лага число пар уровней, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается целесообразным использовать коэффициенты автокорреляции с порядками: 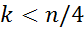 .
.
 2015-05-18
2015-05-18 469
469








