· некоррелированными
· автокоррелированными
· не гетероскедастичными
· гомоскедастичными
Вычислите доверительный интервал с вероятностью 95 % для коэффициента регрессии для модели 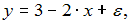 построенной на основании 20 наблюдений, если известны t -статистики для параметров регрессии
построенной на основании 20 наблюдений, если известны t -статистики для параметров регрессии 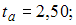
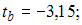 и критическое значение t -критерия
и критическое значение t -критерия 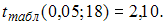
· 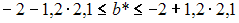
· 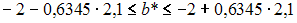
· 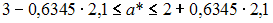
· 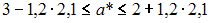
На рисунке представлен график остатков некоторой модели регрессии. Для оценок параметров данной модели регрессии нарушено свойство … 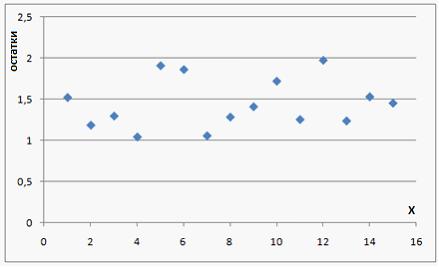
· нормального распределения остатков
· несмещенности
· состоятельности
· эффективности
Регрессионная модель 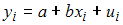 с гетероскедастичными остатками
с гетероскедастичными остатками 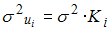 может быть записана в виде _____, где
может быть записана в виде _____, где 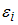 – гомоскедастичные остатки.
– гомоскедастичные остатки.
· 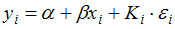
· 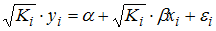
· 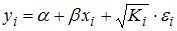
· 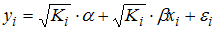
Имеется модель регрессии, характеризующая зависимость y от x 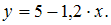 Известны среднеквадратичные отклонения для переменных и количество наблюдений:
Известны среднеквадратичные отклонения для переменных и количество наблюдений: 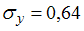 ,
, 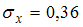 и
и 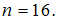 Вычислите коэффициент корреляции
Вычислите коэффициент корреляции 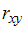 и сделайте вывод относительно тесноты связи между y и x.
и сделайте вывод относительно тесноты связи между y и x.
· 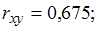 теснота связи средняя, зависимость прямая
теснота связи средняя, зависимость прямая
· 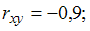 теснота связи сильная, зависимость обратная
теснота связи сильная, зависимость обратная
· 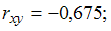 теснота связи средняя, зависимость обратная
теснота связи средняя, зависимость обратная
· 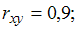 теснота связи сильная, зависимость прямая
теснота связи сильная, зависимость прямая
Интерпретация параметра b: «если x увеличится на 1 %, то y изменится на b %» соответствует модели нелинейной регрессии, выраженной …
· показательной функцией 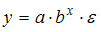
· параболой второго порядка 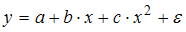
· гиперболой 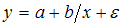
· степенной функцией 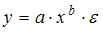
Для нелинейной зависимости значение индекса корреляции составило 0,81, тогда значение индекса детерминации составит …
· 81 %
· 0,9
· 0,656
· 0,19
На рисунке представлен график временного ряда за 4 года (по кварталам). Известны коэффициенты автокорреляции до пятого порядка включительно: 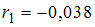 ,
, 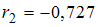 ,
, 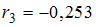 ,
, 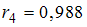 ,
, 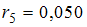 . В состав временного ряда входят …
. В состав временного ряда входят … 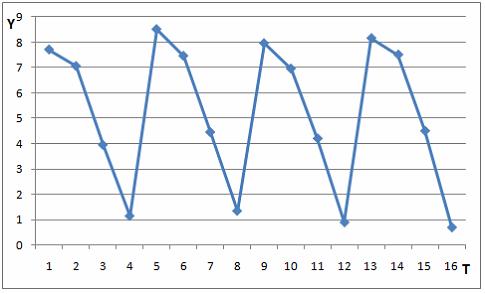
· трендовая компонента, сезонная компонента, случайная компонента
· сезонная компонента, случайная компонента
· трендовая компонента, сезонная компонента
· трендовая компонента, случайная компонента
Для изучения зависимости затрат на производство y (тыс. руб.) от объема выпуска x (шт.) по 8 наблюдениям построены варианты уравнения регрессии и рассчитаны коэффициенты детерминации. Выберите модель регрессии, все параметры которой имеют четкую экономическую интерпретацию.
· 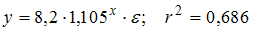
· 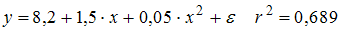
· 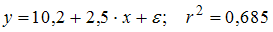
· 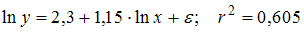
Для уравнения регрессии 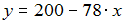 выберите отклонение выборочного (фактического) значения от расчетного для точки с координатами (2; 50).
выберите отклонение выборочного (фактического) значения от расчетного для точки с координатами (2; 50).
· 4
· 44
· 58
· 6
На рисунке представлен график остатков некоторой модели регрессии. Для оценок параметров данной модели регрессии нарушено свойство … 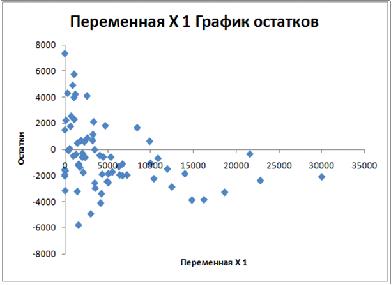
· смещенности
· несмещенности
· состоятельности
· эффективности
Для регрессионной модели 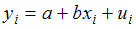 выявлено, что остатки являются гетероскедастичными, при этом дисперсия остатков находится в зависимости от значения фактора с коэффициентом пропорциональности Кi, то есть
выявлено, что остатки являются гетероскедастичными, при этом дисперсия остатков находится в зависимости от значения фактора с коэффициентом пропорциональности Кi, то есть 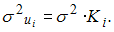 Тогда для исключения гетероскедастичности следует оценивать параметры уравнения …
Тогда для исключения гетероскедастичности следует оценивать параметры уравнения …
· 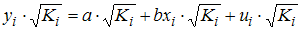
· 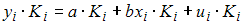
· 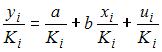
· 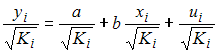
Для уравнения множественной линейной регрессии с двумя регрессорами, рассчитанного на основании 14 наблюдений, коэффициент множественной корреляции равен 0,5. Вычислите значение F-статистики и проверьте значимость построенного уравнения, если 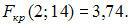
· 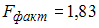 ; построенное уравнение незначимо
; построенное уравнение незначимо
· 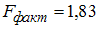 ; уравнение в целом значимо
; уравнение в целом значимо
· 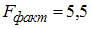 ; построенное уравнение значимо
; построенное уравнение значимо
· 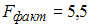 ; уравнение в целом значимо
; уравнение в целом значимо
На рисунке представлен график временного ряда (модельные данные). Известны коэффициенты автокорреляции до пятого порядка включительно: 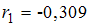 ,
, 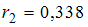 ,
, 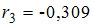 ,
, 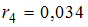 ,
, 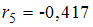 . В состав временного ряда входят …
. В состав временного ряда входят … 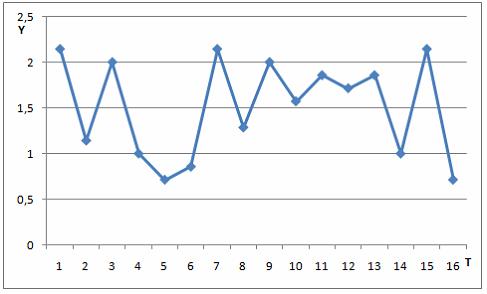
· трендовая компонента, случайная компонента
· случайная компонента
· сезонная компонента
· трендовая компонента
При выраженной сезонной компоненте, амплитуда колебаний которой или монотонно возрастает, или монотонно убывает, строят …
· модель с распределенным лагом
· мультипликативную модель
· аддитивную моделью
· модель, включающей фактор времени
Промежуточные расчеты для 32 пар наблюдений (x, y) дали следующие результаты: 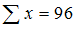 ,
, 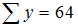 ,
, 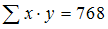 ,
, 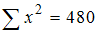 ,
, 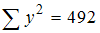 . Оцените параметры регрессии y=a+b∙x+ε из системы нормальных уравнений
. Оцените параметры регрессии y=a+b∙x+ε из системы нормальных уравнений 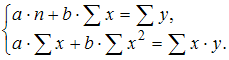
· 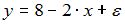
· 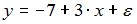
· 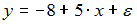
· 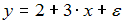
Известно, что в уравнении множественной линейной регрессии 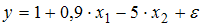 все коэффициенты значимы. Также даны коэффициенты парной корреляции
все коэффициенты значимы. Также даны коэффициенты парной корреляции 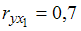 и
и 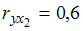 . Самым коротким отрезком, содержащим коэффициент множественной корреляции
. Самым коротким отрезком, содержащим коэффициент множественной корреляции 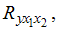 является интервал …
является интервал …
· [0,6;1]
· [0;1]
· [0,7;1]
· [0,6; 0,7]
На рисунке представлен график временного ряда стоимости некоторой ценной бумаги за 16 дней. Известны коэффициенты автокорреляции до пятого порядка включительно: 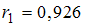 ,
, 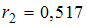 ,
, 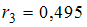 ,
, 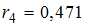 ,
, 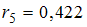 . В состав временного ряда входят …
. В состав временного ряда входят … 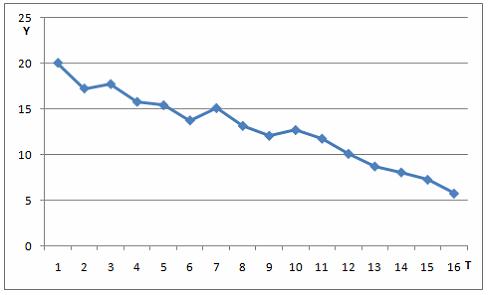
· трендовая компонента, случайная компонента
· сезонная компонента, случайная компонента
· трендовая компонента
· случайная компонента
На рисунке представлен график временного ряда объемов авиаперевозок за 4 года (по кварталам). Известны коэффициенты автокорреляции до пятого порядка включительно: 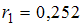 ,
, 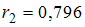 ,
, 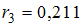 ,
, 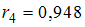 ,
, 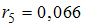 . В состав временного ряда входят …
. В состав временного ряда входят … 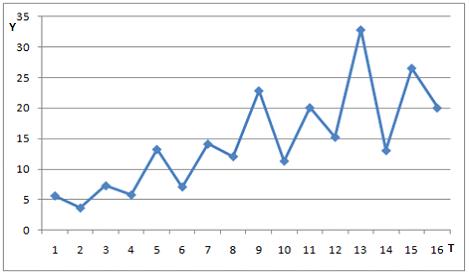
· трендовая компонента, случайная компонента
· сезонная компонента, случайная компонента
· трендовая компонента, сезонная компонента, случайная компонента
· трендовая компонента, сезонная компонента
Системой уравнений, описывающей спрос и предложение и позволяющей учесть три закономерности: 1) зависимость объема спроса 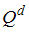 от цены P, 2) зависимость объема предложения
от цены P, 2) зависимость объема предложения 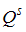 от цены P и 3) тождественное равенство объемов спроса
от цены P и 3) тождественное равенство объемов спроса 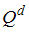 и предложения
и предложения 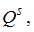 будет система _______ уравнений.
будет система _______ уравнений.
· независимых
· нормальных
· рекурсивных
· одновременных
Если для модели параметров с гетероскедастичными остатками ui необходимо оценить параметры модели вида 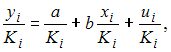 следовательно была выдвинута гипотеза о том что дисперсия остатков модели пропорциональна величине …
следовательно была выдвинута гипотеза о том что дисперсия остатков модели пропорциональна величине …
· 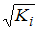
· 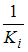
· 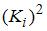
· 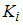
Найдите объясненную дисперсию на одну степень для уравнения множественной линейной регрессии с двумя регрессорами, рассчитанного на основании 23 наблюдений, если общая сумма квадратов отклонений равна 120, а остаточная сумма квадратов равна 30.
· 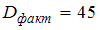
· 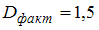
· 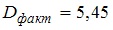
· 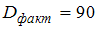
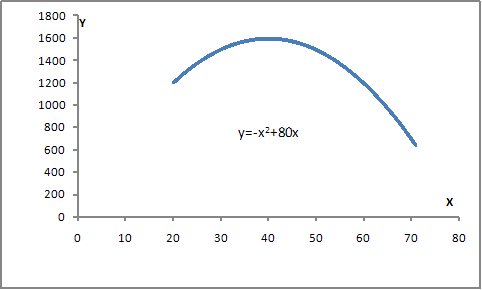
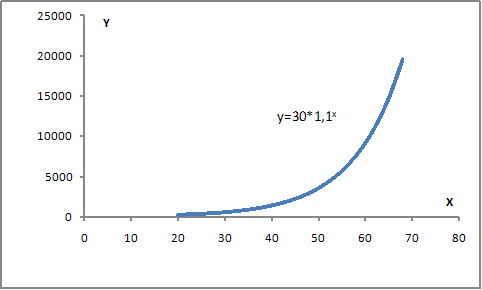
В экономике труда замечено, что с увеличением возраста повышается заработная плата работников физического труда ввиду увеличения опыта и квалификации работника. Однако с определенного возраста ввиду старения организма и снижения производительности труда дальнейшее увеличение возраста приводит к снижению заработной платы работника. Данную зависимость можно описать с помощью …
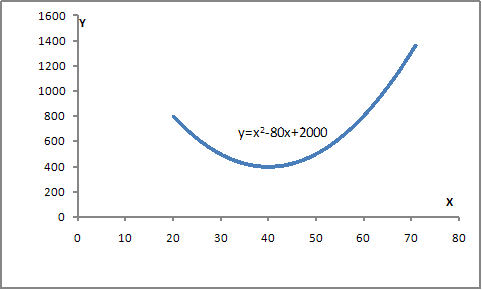
· параболы второго порядка 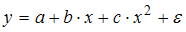 , например, представленной на рисунке,
, например, представленной на рисунке, 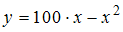
· Гиперболы 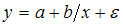 , например, представленной на рисунке,
, например, представленной на рисунке, 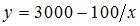
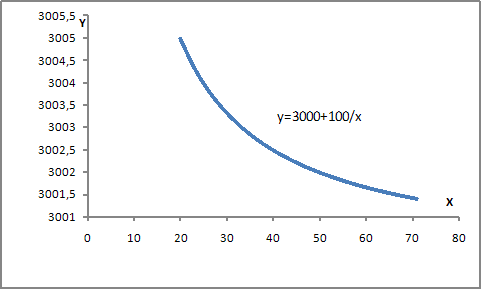
· параболы второго порядка 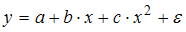 , например, представленной на рисунке
, например, представленной на рисунке 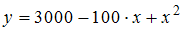
· показательной функции 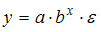 , например, представленной на рисунке,
, например, представленной на рисунке, 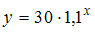
На рисунке отображено поле корреляции для нелинейной зависимости. 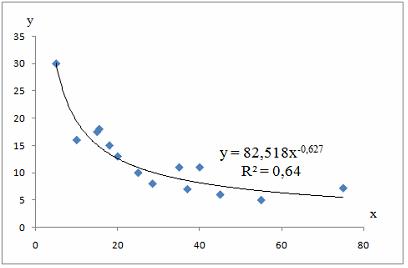 Значение индекса корреляции для указанной модели составляет …
Значение индекса корреляции для указанной модели составляет …
· 0,64
· 0,8
· -0,627
· (0,64)2
Системой уравнений, позволяющей описать функционирование экономики на макроуровне, например, с одной стороны, зависимость частного потребления C от национального дохода Y, и тождественное равенство национального дохода Y сумме частного потребления C и инвестиций I, с другой стороны, будет система ____________ уравнений.
· независимых
· нормальных
· одновременных
· рекурсивных
На рисунке представлены графики остатков линейной и нелинейной функции, построенных по некоторым исходным данным. Относительно свойств несмещенности и эффективности можно сказать, что оценки параметров нелинейной зависимости являются … 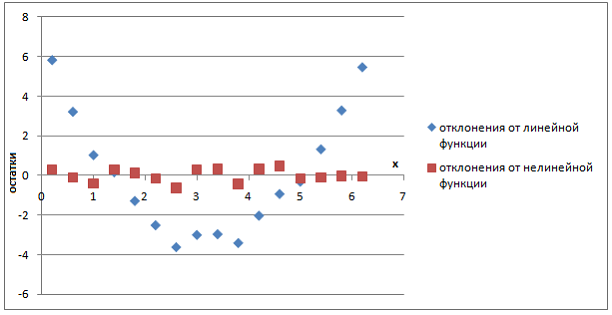
· несмещенными и эффективными
· несмещенными и неэффективными
· смещенными и эффективными
· смещенными и неэффективными
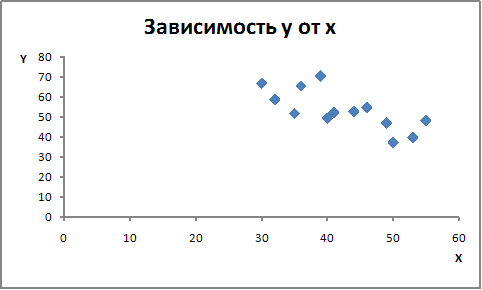
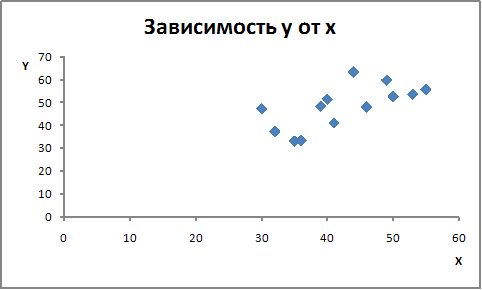
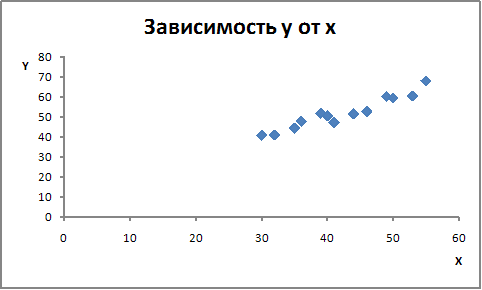
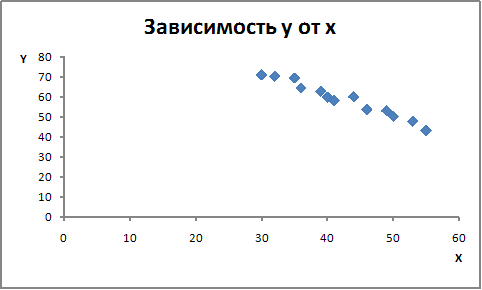
Выберите поле корреляции, соответствующее зависимости между х и у, если известно, что зависимость между переменными обратная (при увеличении х значение у уменьшается) и теснота связи сильная.
· 
· 
· 
· 
Для модели регрессии, построенной на основании n наблюдений и содержащей m независимых уравнений, число степеней свободы для остаточной суммы квадратов отклонений равно …
· n–m–1
· n–m
· n–1
· n–2
Английский экономист А. В. Филлипс, анализируя данные по Англии с 1849 по 1953 гг., установил обратную зависимость процента прироста заработной платы y от уровня безработицы x. Данную нелинейную зависимость можно выразить с помощью …
· параболы второго порядка 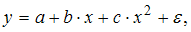 например, представленной на графике
например, представленной на графике 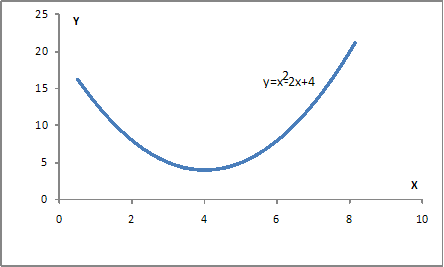
· cтепенная функции 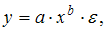 например, представленной на графике
например, представленной на графике 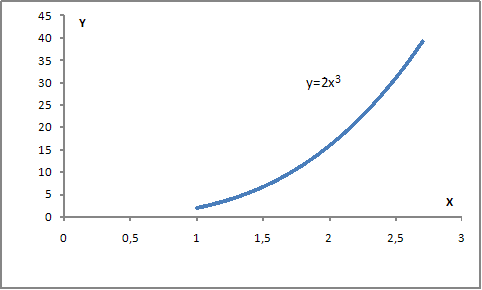
· показательной функции 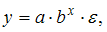 например, представленной на графике
например, представленной на графике 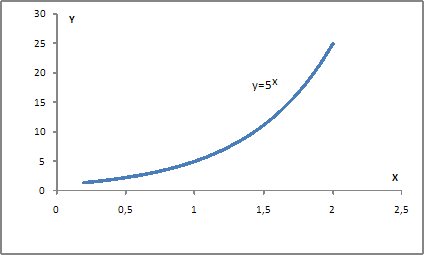
· гиперболы 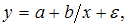 например, представленной на графике
например, представленной на графике 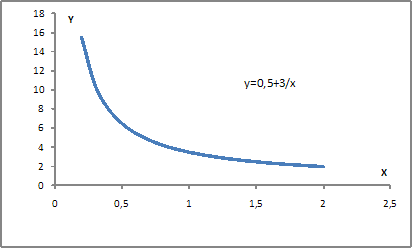
Известно, что зависимость между y и x обратная и связь сильная. Самым коротким отрезком, содержащим коэффициент корреляции 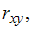 является …
является …
· [0,8;1]
· [–1;0]
· [–1;–0,8]
· [–1;1]
При исследовании зависимости затрат на производство (у, тыс. руб.) от объема выпуска (х, тыс. ед.) построена система нормальных уравнений 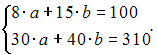 Выберите интерпретацию коэффициента регрессии.
Выберите интерпретацию коэффициента регрессии.
· При увеличении объема выпуска на 1 % затраты на производство увеличиваются на 4 %
· При увеличении объема выпуска на 1 % затраты на производство увеличиваются на 5 %
· При увеличении объема выпуска на 1 тысячу единиц затраты на производство увеличиваются на 5 тысяч рублей
· При увеличении объема выпуска на 1 тысячу единиц затраты на производство увеличиваются на 4 тысячи рублей
На графике представлены: поле корреляции, график линейной зависимости и график нелинейной зависимости, рассчитанные методом наименьших квадратов по исходным данным. Относительно свойств несмещенности и эффективности можно сказать, что оценки параметров линейной зависимости являются … 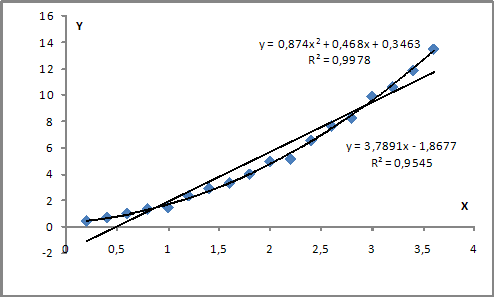
· несмещенными и неэффективными
· смещенными и эффективными
· смещенными и неэффективными
· несмещенными и эффективными
При применении обобщенного метода наименьших квадратов для оценки параметров модели с гетероскедастичными остатками 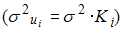 минимизируется величина остаточной дисперсии S, равная …
минимизируется величина остаточной дисперсии S, равная …
· 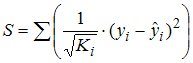
· 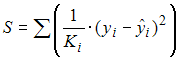
· 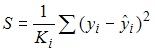
· 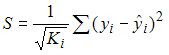
При применении обобщенного метода наименьших квадратов для оценки параметров модели с гетероскедастичными остатками 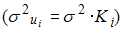 минимизируется величина остаточной дисперсии S, равная …
минимизируется величина остаточной дисперсии S, равная …
· 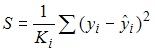
· 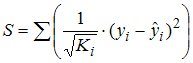
· 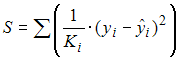
· 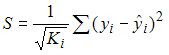
На рисунке представлен график временного ряда объемов авиаперевозок за 4 года (по кварталам). 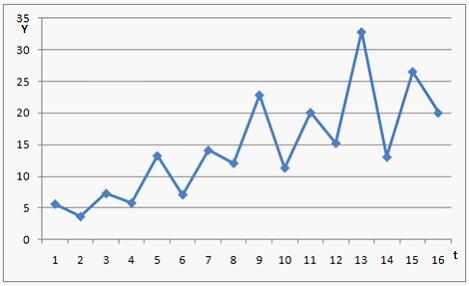 Известны коэффициенты автокорреляции до пятого порядка включительно:
Известны коэффициенты автокорреляции до пятого порядка включительно: 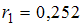 ,
, 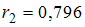 ,
, 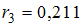 ,
, 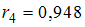 ,
, 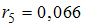 . Обозначим Y – уровень ряда, T – трендовая компонента, S – сезонная компонента, E – случайная компонента. Модель вида __________ позволяет лучше всего учесть обнаруженную сезонную компоненту.
. Обозначим Y – уровень ряда, T – трендовая компонента, S – сезонная компонента, E – случайная компонента. Модель вида __________ позволяет лучше всего учесть обнаруженную сезонную компоненту.
· 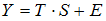
· 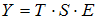
· 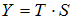
· 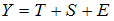
 2015-05-18
2015-05-18 4951
4951