Спецификация переменных модели множественной линейной регрессии – определение состава переменных, которые должны быть включены в модель. Отобранные факторы должны быть количественно измеримы. Неправильная спецификация переменных может произойти из-за не включения в уравнения переменной, которая должна быть в составе объясняющих переменных. Ошибки имеют следующие спецификации.
1) Невключение в модель существенных переменных. Допустим вместо истинной модели y=Xβ+Zɣ+ɛ, взята модель y=Xβ+ɛ.
В модели 2 опущены объясняющие переменные z1.z2…zm. для нее оценка вектора коэффициентов β по методу мнк дается формулой 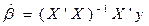 .
.
Представим эту в формулу значение у из истенной модели и найдем мат ожидание: 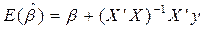 .
.
Последнее выражение равно β лишь в двух случаях. Первый если ɣ=0, т.е на самом деле в истинной модели на зависимую переменную не влияют регрессоры z1,z2,…,zm. Второй если X’Z-нулевая матрица, что означает ортогональность регрессоров x1,x2,…,xk z1,z2,…,zm. Во всех остальных случаях 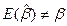 ,т.е оценка
,т.е оценка 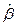 оказывается смещенной.
оказывается смещенной.
2) Включение в модель несущественных переменных. В этом случае истинная модель y=Xβ+ɛ,а модель y=Xβ+Zɣ+ɛ содержит избыточные переменные z1,z2,…,zm. Оценка вектора коэффициентов модели с избыточными переменными по мнк:
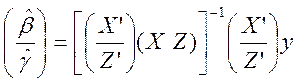 , =>
, => 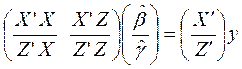 =>
=>
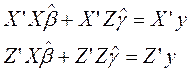
Столбцы матрицы Я линейно независимы. Существует обратная матрица 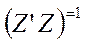 .
.
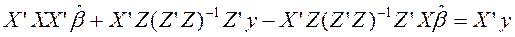 . Перегруппировываем
. Перегруппировываем
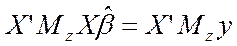 , где матрица
, где матрица 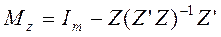 и найдем оценку
и найдем оценку 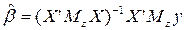 . Теперь определим ожидаемое значение
. Теперь определим ожидаемое значение
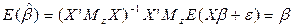 . Следовательно оценка
. Следовательно оценка 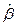 несмещенная. Ее ковариационная матрица
несмещенная. Ее ковариационная матрица 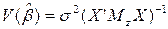 .
.
 2015-05-18
2015-05-18 677
677








