2015-05-18
293
1.3.1.1. Оценка коэффициентов обобщенной регрессии:
.
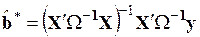1.3.1.2. Тест Уайта. Сначала с помощью обычного МНК строится регрессионная модель, и находятся остатки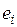 
, 
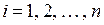. После чего строится регрессия квадратов этих остатков на все регрессоры, их квадраты и попарные произведения. В предположении, что гипотеза 
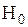(отсутствие гетероскедастичности) имеет место, величина 
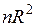асимптотически имеет распределение 
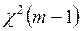, где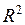 
– коэффициент детерминации, а 
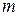– число регрессоров второй модели. Если 
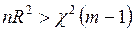, то 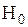отвергается.
1.3.1.3. Тест Голдфельда – Куандта:
1) данные упорядочиваются по убыванию той независимой переменной, от которой в соответствии с предположением зависит дисперсия ошибки;
2) 
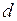наблюдений, расположенных в средине упорядоченного ряда, исключаются ( 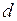рекомендуется брать равным четверти общего числа наблюдений);
3) по первым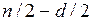 
и последним 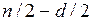строятся независимо друг от друга два регрессионных уравнения и с их помощью рассчитываются соответствующие вектора остатков 
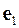и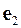 
;
4) из полученных остатков рассчитывается статистика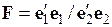 
. Если верна гипотеза 
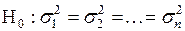, то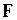 
имеет распределение Фишера с 
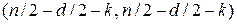степенями свободы. Если статистика больше табличного значения, то гипотеза 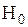отвергается.
1.3.1.4. Тест Бреуша – Пагана:
1) строится обычная регрессия и с ее помощью рассчитываются компоненты вектора остатков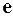 
;
2) рассчитывается оценка дисперсии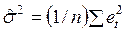 
;
3) строится регрессионное уравнение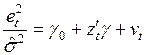 
,
где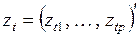 
– вектор независимых переменных; 
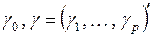– неизвестные параметры.
Для этого уравнения рассчитывается объясненная часть вариации, т.е. сумма квадратов отклонений расчетных значений от среднего значения, обозначаемая обычно RSS;
4) статистика RSS/2 сравнивается с табличным значением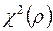 
и, если RSS/2 превосходит табличное значение, то нуль-гипотеза (отсутствие гетероскедастичности) отбрасывается.
