Задание 2.2.1. Руководство одного из крупнейших коммерческих банков ОАО «Александрит» ищет пути уменьшения расходов, связанных с основным видом деятельности – размещением вкладов физических лиц. С этой целью было решено проанализировать, в какой мере среднеквартальное число клиентов (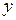 ) определяется величиной затрат на рекламу
) определяется величиной затрат на рекламу 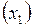 и суммой расходов на связи с общественностью
и суммой расходов на связи с общественностью 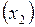 . Данные об этих показателях за последние 20 кварталов представлены в табл. 2.2.1.
. Данные об этих показателях за последние 20 кварталов представлены в табл. 2.2.1.
Т а б л и ц а 2.2.1
 | 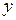 | 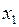 | 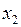 | 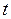 | 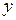 | 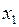 | 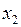 |
| 11,2 | 236,25 | ||||||
| 15,4 | 57,75 | 68,6 | 257,25 | ||||
| 93,75 | 288,75 | ||||||
| 32,2 | 120,75 | 78,2 | 293,25 | ||||
| 127,5 | 281,25 | ||||||
| 38,6 | 144,75 | 303,75 | |||||
| 153,75 | 82,8 | 310,5 | |||||
| 51,2 | 326,25 | ||||||
| 58,4 | 92,4 | 346,5 |
Решение с помощью табличного процессора Excel
1. Ввод исходных данных.
2. Построение регрессионного уравнения с использованием «Пакета анализа» (рис. 2.2.1).
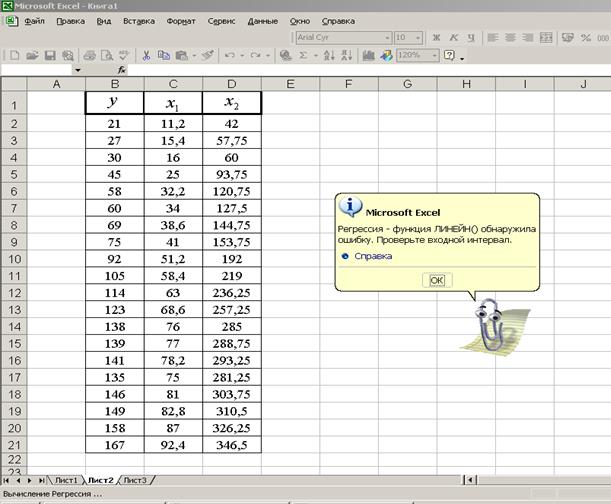
Р и с. 2.2.1. Диалоговое окно инструмента «Регрессия»
3. Полученный результат позволяет выдвинуть гипотезу о наличии эффекта мультиколлинеарности.
3.1. Формирование матрицы 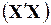 с помощью функций ТРАНСП и МУМНОЖ
с помощью функций ТРАНСП и МУМНОЖ
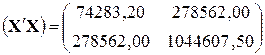 .
.
3.2. Вычисление определителя матрицы 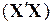 с помощью функции МОПРЕД и по формуле
с помощью функции МОПРЕД и по формуле
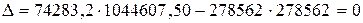 .
.
Равенство определителя нулю говорит о наличии явления мультиколлинеарности в строгом смысле. Следовательно, необходимо исключить один из факторов и перестроить модель заново.
4. Построение регрессионной модели с единственным фактором – расходами на связи с общественностью (см. Вывод итогов 2.2.1).
| ВЫВОД ИТОГОВ 2.2.1 | |||||||
| Регрессионная статистика | |||||||
| Множественный R | 0,999897 | ||||||
| R-квадрат | 0,999793 | ||||||
| Нормированный R-квадрат | 0,999782 | ||||||
| Стандартная ошибка | 0,70675 | ||||||
| Наблюдения | |||||||
| Дисперсионный анализ | |||||||
| df | SS | MS | F | Значимость F | |||
| Регрессия | 43487,81 | 43487,81 | 87063,55 | 1,28E-34 | |||
| Остаток | 8,99091 | 0,499495 | |||||
| Итого | 43496,8 | ||||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Значе-ние | Нижние 95% | Верхние 95% | ||
| Y-пересечение | -0,05655 | 0,372888 | -0,15166 | 0,881139 | -0,83996 | 0,726857 | |
| Переменная X 1 | 0,481433 | 0,001632 | 295,0653 | 1,28E-34 | 0,478005 | 0,484861 | |
Таким образом, построенная модель имеет вид
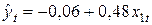 .
.
Высокое значение коэффициента корреляции свидетельствует о существенной взаимосвязи моделируемого показателя с фактором. Сравнение расчетного значения 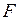 -критерия с табличным
-критерия с табличным 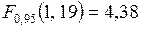 позволяет сделать вывод об адекватности построенной модели. Сравнение расчетных значений t -статистик с табличным
позволяет сделать вывод об адекватности построенной модели. Сравнение расчетных значений t -статистик с табличным 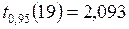 говорит о значимости включенного в модель фактора
говорит о значимости включенного в модель фактора 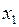 .
.
Задание 2.2.2. Известно, что стоимость выпуска газеты в значительной степени определяется величиной типографских расходов. Для того чтобы иметь возможность воздействовать на эту стоимость, издатели наиболее популярных газет решили изучить факторы, определяющие сумму годовых затрат на печать газет, и оценить степень их влияния. С этой целью для 20 городов России были собраны данные о годовых расходах на печать (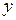 , млн. руб.), объемах розничной продажи газет в городе (млн. руб.) и количества семей в городе (в тысячах). Заметим, что для факторов были взяты их логарифмы (
, млн. руб.), объемах розничной продажи газет в городе (млн. руб.) и количества семей в городе (в тысячах). Заметим, что для факторов были взяты их логарифмы (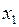 и
и 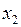 , соответственно) с целью уменьшения разброса данных, а следовательно, и упрощения их обработки. Все эти данные представлены в табл. 2.2.2. Постройте модель множественной регрессии, отражающую зависимость среднегодовых расходов на издание газеты от соответствующих факторов.
, соответственно) с целью уменьшения разброса данных, а следовательно, и упрощения их обработки. Все эти данные представлены в табл. 2.2.2. Постройте модель множественной регрессии, отражающую зависимость среднегодовых расходов на издание газеты от соответствующих факторов.
Решение с помощью табличного процессора Excel
1. Ввод исходных данных.
Т а б л и ц а 2.2.2
| № п.п. | 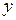 | 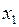 | 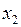 | № п.п. | 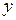 | 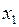 | 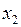 |
| 1. | 2,8 | 4,4 | 3,00 | 11. | 2,7 | 4,24 | 2,89 |
| 2. | 2,3 | 3,68 | 2,51 | 12. | 2,9 | 4,72 | 3,22 |
| 3. | 2,5 | 3,92 | 2,67 | 13. | 3,3 | 5,28 | 3,6 |
| 4. | 2,7 | 4,32 | 2,94 | 14. | 2,7 | 4,24 | 2,89 |
| 5. | 2,6 | 4,24 | 2,89 | 15. | 1,8 | 3,04 | 2,07 |
| 6. | 2,4 | 3,76 | 2,56 | 16. | 1,9 | 3,12 | 2,13 |
| 7. | 3,5 | 5,52 | 3,76 | 17. | 2,2 | 3,6 | 2,46 |
| 8. | 2,1 | 3,36 | 2,29 | 18. | 2,3 | 3,68 | 2,51 |
| 9. | 1,9 | 3,04 | 2,07 | 19. | 3,6 | 5,76 | 3,92 |
| 10. | 3,8 | 5,92 | 4,03 | 20. | 2,2 | 3,6 | 2,45 |
2. Построение регрессионного уравнения с использованием «Пакета анализа» (см. Вывод итогов 2.2.2) и анализ полученных результатов.
| ВЫВОД ИТОГОВ 2.2.2 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,997299 | |||||
| R-квадрат | 0,994606 | |||||
| Нормированный R-квадрат | 0,993972 | |||||
| Стандартная ошибка | 0,044773 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 6,283922 | 3,141961 | 1567,374 | 5,26E-20 | ||
| Остаток | 0,034078 | 0,002005 | ||||
| Итого | 6,318 | |||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Значе-ние | Нижние 95% | Верхние 95% | |
| Y-пересечение | -0,10201 | 0,052759 | -1,93359 | 0,069992 | -0,21333 | 0,009298 |
| Переменная X 1 | 2,653207 | 2,446084 | 1,084675 | 0,293209 | -2,50759 | 7,814002 |
| Переменная X 2 | -2,93956 | 3,595708 | -0,81752 | 0,424942 | -10,5258 | 4,646732 |
Анализ вывода итогов 2.2.2 свидетельствует о том, что полученные стандартные ошибки значительно больше самих расчетных коэффициентов. Коэффициенты при факторах 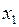 и
и 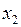 незначимы, так как для них P-значениябольше 0,05. В то же время сравнение расчетного значения
незначимы, так как для них P-значениябольше 0,05. В то же время сравнение расчетного значения 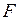 -критерия с табличным
-критерия с табличным 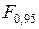 (2, 17) = 3,59 позволяет сделать вывод об адекватности рассматриваемой модели.
(2, 17) = 3,59 позволяет сделать вывод об адекватности рассматриваемой модели.
Коэффициенты корреляции говорят о существенной взаимосвязи моделируемого показателя с факторами (см. табл. 2.2.3, полученную в результате выполнения действий, указанных на рис. 2.2.2). Одной из причин противоречивости результатов модели является тесная взаимосвязь между факторами. Все эти факты говорят о том, что изучаемая модель требует более детального анализа.
 |
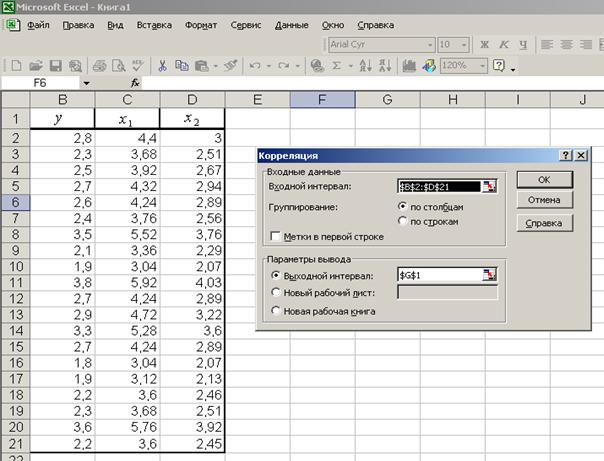 |
Р и с. 2.2.2. Построение корреляционной матрицы
с помощью пакета «Анализ данных» MS Excel
Т а б л и ц а 2.2.3
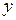 | 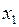 | 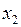 | |
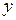 | 0,9972 | 0,9971 | |
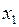 | 0,9972 | 0,9999 | |
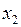 | 0,9971 | 0,9999 |
3. Проверка условия невырожденности матрицы 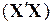 .
.
3.1. Формирование матрицы 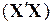 с помощью функций ТРАНСП и МУМНОЖ
с помощью функций ТРАНСП и МУМНОЖ
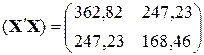 .
.
3.2. Вычисление определителя матрицы 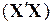 с помощью функции МОПРЕД
с помощью функции МОПРЕД
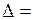 0,0633.
0,0633.
Близость определителя к нулю, а также проведенный выше анализ позволяют сделать вывод о наличии частичной мультиколлинеарности.
4. Устранение эффекта мультиколлинеарности с помощью ридж-оценивания.
4.1. Включение в модель дополнительной переменной 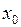 , принимающей единственное значение, равное 1.
, принимающей единственное значение, равное 1.
4.2. Расчет коэффициентов регрессии с использованием матричных функций Excel.
4.2.1. Формирование матрицы, обратной к матрице системы нормальных уравнений 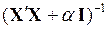 с помощью функций ТРАНСП, МУМНОЖ и МОБР при
с помощью функций ТРАНСП, МУМНОЖ и МОБР при 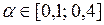 .
.
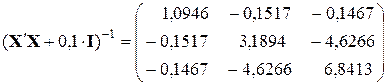 ;
; 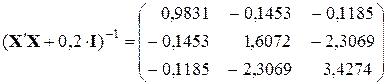 ;
;
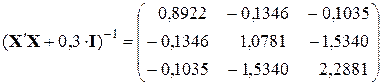 ;
;
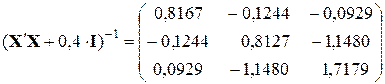 .
.
4.2.2. Получение вектора оценок коэффициентов регрессии путем умножения обратной матрицы на матрицы 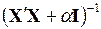 и
и 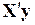 при различных значениях
при различных значениях 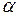 . Оформление результатов виде табл. 2.2.4.
. Оформление результатов виде табл. 2.2.4.
5. Расчет стандартных ошибок коэффициентов регрессии.
5.1. Вычисление остаточной дисперсии при различных значениях 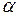 и оформление результатов расчетов в виде табл. 2.2.5.
и оформление результатов расчетов в виде табл. 2.2.5.
Т а б л и ц а 2.2.4
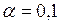 | 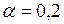 | 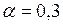 | 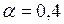 | |
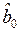 | -0,0937 | -0,0745 | -0,0588 | -0,0458 |
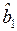 | 0,4454 | 0,4411 | 0,4381 | 0,4358 |
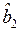 | 0,2975 | 0,2972 | 0,2961 | 0,2950 |
Т а б л и ц а 2.2.5
| Квадраты отклонений расчетных от фактических значений | |||
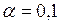 | 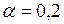 | 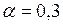 | 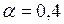 |
| 0,001703 | 0,001766 | 0,001826 | 0,001884 |
| 0,000060 | 0,000028 | 0,000011 | 0,000003 |
| 0,002836 | 0,002686 | 0,002576 | 0,002493 |
| 0,000028 | 0,000024 | 0,000020 | 0,000016 |
| 0,002997 | 0,002993 | 0,002980 | 0,002961 |
| 0,003277 | 0,003036 | 0,002854 | 0,002715 |
| 0,000265 | 0,000489 | 0,000728 | 0,000970 |
| 0,000248 | 0,000139 | 0,000074 | 0,000037 |
| 0,000564 | 0,000336 | 0,000195 | 0,000109 |
| 0,003337 | 0,004280 | 0,005152 | 0,005956 |
| 0,002048 | 0,002051 | 0,002062 | 0,002078 |
| 0,004453 | 0,004163 | 0,003920 | 0,003714 |
| 0,000854 | 0,000599 | 0,000420 | 0,000292 |
| 0,002048 | 0,002051 | 0,002062 | 0,002078 |
| 0,005815 | 0,006670 | 0,007400 | 0,008024 |
| 0,000885 | 0,001211 | 0,001509 | 0,001776 |
| 0,001742 | 0,001989 | 0,002196 | 0,002368 |
| 0,000060 | 0,000028 | 0,000011 | 0,000003 |
| 0,001462 | 0,000980 | 0,000653 | 0,000426 |
| 0,001502 | 0,001733 | 0,001927 | 0,002090 |
| Сумма квадратов отклонений расчетных от фактических значений | |||
| 0,036183 | 0,037251 | 0,038577 | 0,039994 |
| Остаточная дисперсия | |||
| 0,002128 | 0,002191 | 0,002269 | 0,002353 |
5.2. Получение стандартных ошибок в виде корня квадратного из произведения диагональных элементов обратной матрицы на остаточную дисперсию при различных значениях 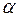 . Оформление результатов расчетов в виде табл. 2.2.6.
. Оформление результатов расчетов в виде табл. 2.2.6.
Т а б л и ц а 2.2.6
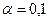 | 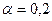 | 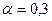 | 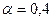 | |
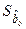 | 0,0483 | 0,0464 | 0,0450 | 0,0438 |
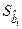 | 0,0824 | 0,0593 | 0,0495 | 0,0437 |
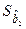 | 0,1207 | 0,0867 | 0,0721 | 0,0636 |
Таким образом, наименьшая стандартная ошибка получена при 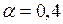
Следовательно, построенная модель может быть записана в виде
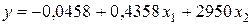 .
.
6. Проверка значимости полученных коэффициентов регрессии
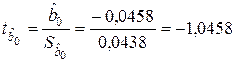 ;
; 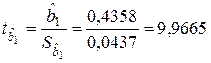 ;
; 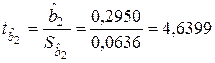 .
.
Сравнение расчетных значений t -статистик с табличным 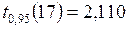 свидетельствует о значимости включенных в модель факторов
свидетельствует о значимости включенных в модель факторов 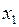 и
и 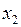 .
.
 2015-05-18
2015-05-18 1071
1071








