Задание 4.4.2.1. По данным табл. 4.4.2.1, характеризующим объем продаж спортивного оборудования для футбола, постройте модель ARIMA (p, q, 0), предварительно убедившись на 95%-ном уровне значимости в интеграции данного временного ряда и определив порядок авторегрессии. С помощью построенной модели осуществите прогнозные расчеты на два последующих периода.
Т а б л и ц а 4.4.2.1
| Год | Назначение оборудования: | |||||
| физические упражнения | гольф | кэмпинг | бейсбол | футбол | теннис | |
Решение с помощью табличного процессора Excel.
1. Ввод исходных данных и оформление их в виде табл. 4.4.2.2.
Т а б л и ц а 4.4.2.2
| |||||||||||||
|
2. Проверка временного ряда на стационарность с помощью критерия Дики – Фуллера, т.е. проверка гипотезы
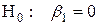 ,
,
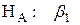 значительно меньше нуля.
значительно меньше нуля.
2.1.Оценка с помощью метода наименьших квадратов (пакета анализа данных Excel) параметров модели 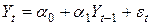
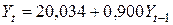 .
.
(9,349) (0,068)
2.2. Расчет статистики
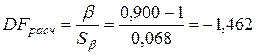
и сравнение ее с критическим значением расширенного критерия Дики – Фуллера на 95%-ном уровне значимости, равным
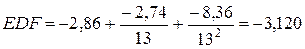 .
.
Для данного уровня значимости ряд нестационарен, так как 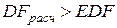 .
.
2.3. Разностное представление временного ряда
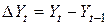
и оформление результатов в виде табл. 4.4.2.3.
Т а б л и ц а 4.4.2.3
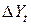
| -1 | -4 | -3 | |||||||||
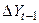
| -1 | -4 | -3 |
2.4. Оценка с помощью метода наименьших квадратов параметров модели 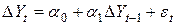
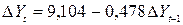 .
.
(2,387) (0,252)
2.5. Расчет статистики
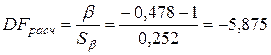
и сравнение ее с критическим значением расширенного критерия Дики – Фуллера на 95%-ном уровне значимости
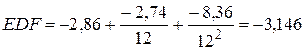 .
.
Для данного уровня значимости ряд стационарен, так как 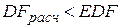 и, следовательно, мы имеем дело с процессом I (1).
и, следовательно, мы имеем дело с процессом I (1).
3. Определение порядка авторегрессии для преобразованного ряда.
3.1. Расчет частных коэффициентов автокорреляции.
Частный коэффициент автокорреляции первого порядка равен коэффициенту автокорреляции первого порядка, т.е. 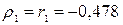 . Частный коэффициент автокорреляции второго порядка равен последнему коэффициенту авторегрессионного уравнения второго порядка, т.е. для его получения необходимо построить авторегрессионное уравнение второго порядка с помощью пакета анализа Excel по данным табл. 4.4.2.4.
. Частный коэффициент автокорреляции второго порядка равен последнему коэффициенту авторегрессионного уравнения второго порядка, т.е. для его получения необходимо построить авторегрессионное уравнение второго порядка с помощью пакета анализа Excel по данным табл. 4.4.2.4.
Т а б л и ц а 4.4.2.4
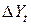
| -1 | -4 | -3 | ||||||||
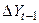
| -1 | -4 | -3 | ||||||||
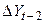
| -1 | -4 |
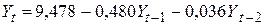 .
.
Получили, что значение частного коэффициента автокорреляции резко падает, следовательно, для преобразованного временного ряда имеет смысл строить модель ARIMA (1,1,0).
3.2. Осуществление прогнозных расчетов по авторегрессионной модели первого порядка, построенной в п. 2.4:
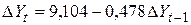 ,
,
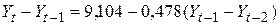 ,
,
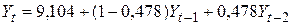 ,
,
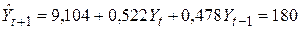 ,
,
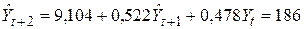 .
.
Задание 4.4.2.2. Руководство плодово-овощного концерна «Витамин», владеющего большими яблоневыми садами в настоящее время желает заглянуть в перспективу, чтобы ответить на вопрос о целесообразности дальнейшего расширения этих садов. С этой целью было решено построить ARMA -модель, с помощью которой получить прогнозные оценки потребления яблок в следующие два года. Данные, отражающие динамику среднегодового потребления яблок населением г. Воронежа (y, т.), представлены в табл. 4.4.2.5.
Т а б л и ц а 4.4.2.5
| T | |||||||||
| Y | |||||||||
| T | |||||||||
| Y | |||||||||
| T | |||||||||
| Y |
Решение табличного процессора Excel
1. Ввод исходных данных и оформление их в удобном для проведения расчетов виде.
2. Настройка параметра 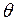 .
.
2.1. Присвоение первоначального значения параметру 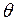
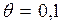 .
.
2.2. Расчет преобразованных значений 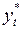 по следующим формулам:
по следующим формулам:
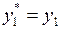 ,
, 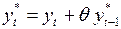 ,
, 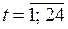 .
.
(Два последних значения будут использоваться в качестве контрольной выборки для настройки параметра 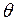 ).
).
2.3. Формирование ряда значений 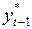 ,
, 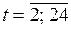 .
.
2.4. Оформление полученных результатов в виде табл. 4.4.2.6.
Т а б л и ц а 4.4.2.6
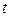
| 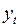
| 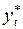
| 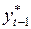
| 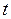
| 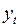
| 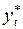
| 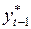
|
| 6521,01 | 6610,13 | ||||||
| 6412,10 | 6521,01 | ||||||
| 5420,80 | 6591,21 | 6412,10 | |||||
| 5452,08 | 5420,80 | 6779,12 | 6591,21 | ||||
| 6405,21 | 5452,08 | 6907,91 | 6779,12 | ||||
| 6400,52 | 6405,21 | 7360,79 | 6907,91 | ||||
| 6590,05 | 6400,52 | 7546,08 | 7360,79 | ||||
| 6779,01 | 6590,05 | 7494,61 | 7546,08 | ||||
| 5727,90 | 6779,01 | 7679,46 | 7494,61 | ||||
| 5712,79 | 5727,90 | 7637,95 | 7679,46 | ||||
| 6401,28 | 5712,79 | 8113,79 | 7637,95 | ||||
| 6610,13 | 6401,28 | 8491,38 | 8113,79 |
2.5. Нахождение текущих значений параметров регрессии
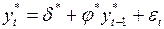 ,
, 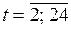
с помощью «Пакета анализа» Excel (см. Вывод итогов 4.4.2.1).
| ВЫВОД ИТОГОВ 4.4.2.1 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,900037 | |||||
| R-квадрат | 0,810067 | |||||
| Нормированный R-квадрат | 0,801023 | |||||
| Стандартная ошибка | 378,3206 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 89,56557 | 5,04E-09 | ||||
| Остаток | 143126,4 | |||||
| Итого | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 683,5531 | 642,6216 | 1,063695 | 0,299546 | -652,852 | 2019,958 |
| Переменная X 1 | 0,919154 | 0,097122 | 9,463909 | 5,04E-09 | 0,717178 | 1,12113 |
Таким образом, 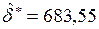 ,
, 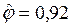 , а сама модель записывается в виде
, а сама модель записывается в виде
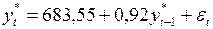 .
.
2.6. Расчет параметров регрессии для исходного ряда
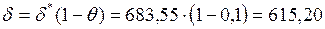 ;
; 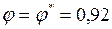 .
.
Следовательно, модель для исходных данных записывается в виде
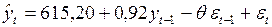 .
.
2.7. Вычисление по построенной модели прогнозных значений 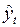 для моментов времени
для моментов времени 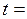 25; 26.
25; 26.
2.8. Определение суммы квадратов отклонений прогнозных от фактических значений потребления яблок.
2.9. Оформление полученных результатов в виде табл. 4.4.2.7.
Т а б л и ц а 4.4.2.7
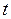
| 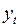
| 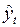
| 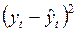
|
| 7674,30 | 21228,71 | ||
| 7802,98 | 5326,19 | ||
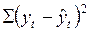
| 26554,91 |
2.10. Последовательное изменение параметра 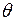 в интервале (0; 1) с шагом 0,1 и проведение всех расчетов п. 2.1-2.9. Оформление промежуточных результатов в виде табл. 4.4.2.8.
в интервале (0; 1) с шагом 0,1 и проведение всех расчетов п. 2.1-2.9. Оформление промежуточных результатов в виде табл. 4.4.2.8.
Т а б л и ц а 4.4.2.8
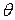
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
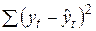
| 26554,9 | 43026,3 | 78931,6 | ||
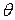
| 0,6 | 0,7 | 0,8 | 0,9 | |
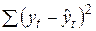
| 53245,1 | 25672,8 |
2.11. Уточнение параметра 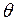 =0,90 с шагом 0,01 и проведение всех расчетов п. 2.1-2.9. Оформление промежуточных результатов в виде табл. 4.4.2.9.
=0,90 с шагом 0,01 и проведение всех расчетов п. 2.1-2.9. Оформление промежуточных результатов в виде табл. 4.4.2.9.
Т а б л и ц а 4.4.2.9
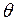
| 0,91 | 0,92 | 0,93 | 0,94 | 0,95 | 0,96 |
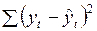
| 25082,25 | 25048,00 | 25615,18 | 26830,12 | 28740,29 | 31393,99 |
Таким образом, оптимальным параметром является 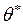 = 0,92.
= 0,92.
3. Построение прогнозной модели с использованием оптимального параметра 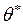 = 0,92 путем последовательного выполнения шагов 2.2. – 2.6 для
= 0,92 путем последовательного выполнения шагов 2.2. – 2.6 для 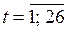 . В результате получится модель, которая записывается в виде
. В результате получится модель, которая записывается в виде
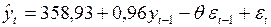 .
.
4. Расчет по построенной модели прогнозных оценок потребления яблок на два года
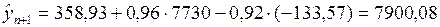 ,
,
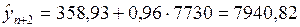 .
.
 2015-05-18
2015-05-18 434
434








