После определения вида функциональной зависимости – у = f(x) оценивают параметры модели. Для определения «наилучших» параметров модели можно использовать следующие критерии:
1) сумму квадратов отклонений наблюдаемых значений зависимой переменной у от значений 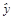 , рассчитанных по функции
, рассчитанных по функции 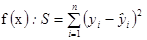 – метод наименьших квадратов (МНК);
– метод наименьших квадратов (МНК);
2) сумму модулей отклонений наблюдаемых значений зависимой переменной от ее расчетных значений: 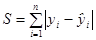 ;
;
3) 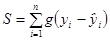 , где g – «мера», с которой отклонение для i-го наблюдения входит в функционал.
, где g – «мера», с которой отклонение для i-го наблюдения входит в функционал.
Оптимальными будут значения параметров, минимизирующие функционал S.
Для оценки параметров bj(j = 0; 1) модели линейной пар ной регрессии: yi =b0 + b1∙xi + ui (i = 1; п) наиболее часто используется традиционный (обычный) метод наименьших квадратов, согласно которому в качестве оценок параметров принимают величины 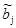 (j = 0; 1), минимизирующие сумму квадратов отклонении наблюдаемых значений результативного признака — yi от расчетных (теоретических) значений –
(j = 0; 1), минимизирующие сумму квадратов отклонении наблюдаемых значений результативного признака — yi от расчетных (теоретических) значений – 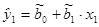 :
:
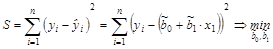
Значения yi и xi (i = 1; п) нам известны, это данные наблюдений. В функции S они представляют собой константы. Переменными в данной функции являются оценки параметров 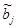 (j = 0; 1). Чтобы найти минимум функции двух переменных, необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их к нулю, т.е.
(j = 0; 1). Чтобы найти минимум функции двух переменных, необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их к нулю, т.е.
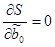 ,
, 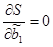 .
.
В результате получим систему из двух нормальных линейных уравнений:
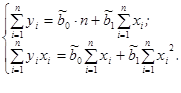
Решая данную систему, найдем искомые оценки пара метров:
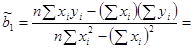
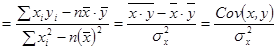
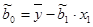
где 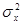 – дисперсия факторного признака;
– дисперсия факторного признака;
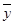 – среднее значение результативного признака;
– среднее значение результативного признака;
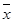 – среднее значение факторного признака;
– среднее значение факторного признака;
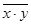 – среднее значение произведения фактора на результат.
– среднее значение произведения фактора на результат.
Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм 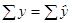 (при этом, возможно некоторое расхождение из-за округления расчетов).
(при этом, возможно некоторое расхождение из-за округления расчетов).
Результаты многих исследований подтверждают, что число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров при переменной х. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла.
Рассмотрим пример: по данным о заработной плате и возрасте 10 рабочих (см. табл. 1.5) оценить параметры линейной парной регрессии методом наименьших квадратов.
Расчет оценки коэффициента регрессии 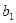 сведем в табл. 1.5.
сведем в табл. 1.5.
Таблица 1.5
| № наблю-дения | X – возраст рабочего, лет | Y – заработная плата за месяц, $ | 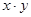 | 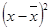 |
| 44,22 | ||||
| 18,92 | ||||
| 0,12 | ||||
| 13,32 | ||||
| 160,02 | ||||
| 87,42 | ||||
| 5,52 | ||||
| 18,92 | ||||
| 205,92 | ||||
| 128,82 | ||||
| 58,52 | ||||
| 31,92 | ||||
| 113,42 | ||||
| 152,52 | ||||
| 31,92 | ||||
| 18,92 | ||||
| 18,92 | ||||
| 5,52 | ||||
| 44,22 | ||||
| 113,42 | ||||
 | 1272,55 | |||
| Среднее значение | 35,65 | 63,63 |
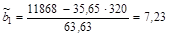
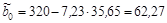
Тогда линейная парная регрессии, описывающая зависимость заработной платы от возраста рабочего: 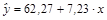
То есть с увеличением возраста рабочего на 1 год работная плата в среднем повышается на 7,23 руб.
В матричной форме критерий метода наименьших квадратов записывается так:
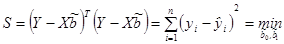
Дифференцируем S по вектору b и приравняем производные 0, чтобы найти МНК-оценки b. В результате получим систему из двух нормальных линейных уравнении:
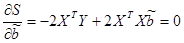 .
.
Учитывая обратимость матрицы 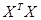 , находим МНК-оценку вектора b:
, находим МНК-оценку вектора b: 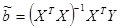 , где
, где 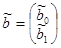 .
.
По правилу умножения матриц:


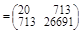 .
.
В матрице ХТХ число 20, лежащее на пересечении 1-й строки и 1-го столбца получено как сумма произведений элементов 1-й строки матрицы ХT и 1-го столбца матрицы X. Число 713, лежащее на пересечении 1-й строки и 2-го столбца, получено как сумма произведений элементов 1-й строки матрицы ХТ и 2-го столбца матрицы X и т. д
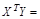
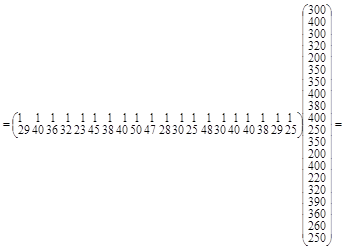
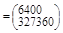 .
.
Найдем обратную матрицу:
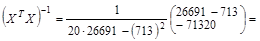
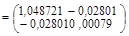 .
.
Тогда вектор оценок параметров регрессии равен:
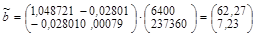 а оценка уравнения регрессии будет иметь вид:
а оценка уравнения регрессии будет иметь вид: 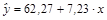
 2015-05-18
2015-05-18 2359
2359
