Нормальная (классическая или традиционная) линейная регрессионная модель с одной переменной (Classical Normal Regression model) — это модель вида: yi =b0 + b1∙xi + ui (i = 1; n), для которой выполняются следующие условия (предпосылки):
1) хi – детерминированная (неслучайная, нестохастическая) величина;
2) М(ui) = 0, (i = 1; n) – математическое ожидание случайной составляющей; равно 0 в любом наблюдении;
3) 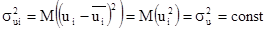 (i = 1; n) – теоретическая дисперсия случайной составляющей; постоянна для всех наблюдений;
(i = 1; n) – теоретическая дисперсия случайной составляющей; постоянна для всех наблюдений;
4) 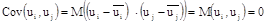
(i # j) – отсутствие систематической связи между значениями случайной составляющей в любых двух наблюдениях (ковариация случайных составляющих в любых двух разных наблюдениях равна нулю);
5) часто добавляется условие: 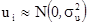 , т. е. ui – нормально распределенная случайная величина.
, т. е. ui – нормально распределенная случайная величина.
Первая предпосылка – сильное предположение. Иногда достаточно сделать предположение о независимости распределения случайной составляющей ui от xi.
Третья предпосылка – о независимости дисперсии случайной составляющей от наблюдения называется гомоскедастичностью (homoscedasticity в переводе означает одинаковый разброс). Случай, когда условие гомоскедастичности не выполняется, называется гетероскедастичностью (heteroscedasticity – неодинаковый разброс).
Четвертая предпосылка указывает на некоррелированность случайных составляющих для разных наблюдений. Это условие нарушается в случае, когда данные являются временными рядами. В случае, когда это условие не выполняется, говорят об автокорреляции случайных составляющих.
Запишем теперь матричную форму нормальной линейной модели парной регрессии.
Y = X ∙ b + u
Предпосылки модели:
1) х — детерминированная (нестохастическая) переменная;
2) 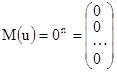
3, 4) третья и четвертая предпосылка в матричной форме могут быть сформулированы через ковариационную матрицу случайных составляющих
Элементами ковариационной матрицы являются показатели ковариации. В общем случае ковариация – 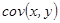 представляет собой показатель тесноты связи между признаками х и у, вычисляемый как среднее из произведений отклонений признаков от их средних значений:
представляет собой показатель тесноты связи между признаками х и у, вычисляемый как среднее из произведений отклонений признаков от их средних значений:
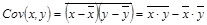
Свойства ковариации:
а) Ковариация переменной и константы равна 0: Cоv(x, A) = 0 (А = const);
б) Ковариация переменной с самой собой равна дисперсии переменной: 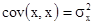 .
.
Для нормальной линейной модели регрессии ковариационная матрица должна иметь вид
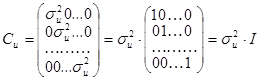
где 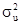 – дисперсия случайной составляющей; I – единичная матрица размером п × п.
– дисперсия случайной составляющей; I – единичная матрица размером п × п.
5) 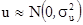 .
.
 2015-05-18
2015-05-18 2387
2387
