1.3.1. Оценка дисперсии случайной составляющей – 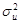 . Статистические свойства МНК-оценок (состоятельность, несмещенность, эффективность). Ковариационная матрица МНК-оценок параметров регрессии
. Статистические свойства МНК-оценок (состоятельность, несмещенность, эффективность). Ковариационная матрица МНК-оценок параметров регрессии
Оценка дисперсии случайной составляющей в случае ной линейной регрессии.
Несмещенной оценкой дисперсии случайной составляющей является:
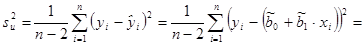
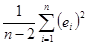
где ei – остаток, равный разности между фактическим и рассчитанным по уравнению регрессии значениями у:
Оценкой ковариационной матрицы случайных составляющих Сu будет матрица: 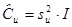 .
.
При повторении выборок того же самого объема n из той же самой генеральной совокупности и при тех же самых значениях объясняющих переменных х наблюдаемые значения зависимой переменной у будут случайным образом варьироваться (за счет случайного характера случайной составляющей u). Следовательно, будут варьироваться и зависеть от у1,.., уn значения оценок параметров регрессии (j = 0; 1] и оценка дисперсии случайной составляющей.
Покажем на примере 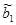 что значение МНК-оценки параметра регрессии зависит от случайной составляющей u.
что значение МНК-оценки параметра регрессии зависит от случайной составляющей u.
МНК-оценка коэффициента регрессии, как было показано в п. 1.2.3, рассчитывается как отношение ковариации x и y к дисперсии х:
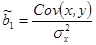
Так как y зависит от случайной составляющей u (y=b0+b1x+u), то ковариация 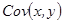 может быть расписана следующим образом:
может быть расписана следующим образом:
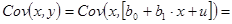
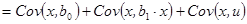 .
.
Причем из свойств ковариации (см п. 1.2.2) следует, что:
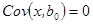 ;
; 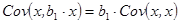 ;
;
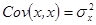 .
.
Тогда 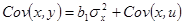 .
.
В результате МНК-оценка может быть разложена на случайную и неслучайную составляющие:
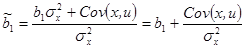 ,
,
т.е. МНК-оценка 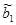 может быть представлена как сумма слагаемых:
может быть представлена как сумма слагаемых:
1) постоянной величины, равной истинному значению коэффициента b1;
2) случайной составляющей Cov(х, u), которая обусловливает отклонения оценки коэффициента регрессии от истинного значения.
Аналогично можно показать, что МНК-оценка 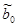 , а так же оценка дисперсии
, а так же оценка дисперсии 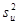 имеют постоянную составляющую, равную истинному значению, и случайную составляющую зависящую от u.
имеют постоянную составляющую, равную истинному значению, и случайную составляющую зависящую от u.
Следует заметить, что на практике мы не можем разложить оценки параметров регрессии и 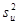 на составляющие, так как истинные значения b0,b1 и
на составляющие, так как истинные значения b0,b1 и 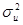 нам не известны, кроме того, мы не знаем фактических значений u в выборке.
нам не известны, кроме того, мы не знаем фактических значений u в выборке.
Однако приведенное выше разложение оценок позволяет получить некоторую теоретическую информацию об их свойствах.
Свойства МНК-оценок. Критериями лучшего способа оценивания является требование состоятельности, несмещенности и эффективности оценок, найденных данным способом.
Способ оценивания дает состоятельные оценки, если при бесконечно большом объеме выборки значение статистической оценки стремится к искомому значению параметра (характеристики) генеральной совокупности.
Способ оценивания дает несмещенные оценки, если математическое ожидание оценки при данном способе оценивания тождественно искомому параметру (характернее генеральной совокупности (при любом объеме выборки).
Оценка, полученная при данном способе оценивания называется эффективной, если ее дисперсия минимальна (при заданном объеме выборки n).
МНК-оценки параметров и дисперсии случайной составляющей являются «наилучшими» (состоятельными, несмещенными и эффективными) оценками.
Докажем, что 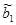 является несмещенной оценкой b1 если выполняется 1-я предпосылка нормальной линейной модели регрессии. Если мы примем сильную форму 1-й предпосылки нормальной линейной регрессионной модели, т.е. предположим, что x –неслучайная величина, то мы можем считать
является несмещенной оценкой b1 если выполняется 1-я предпосылка нормальной линейной модели регрессии. Если мы примем сильную форму 1-й предпосылки нормальной линейной регрессионной модели, т.е. предположим, что x –неслучайная величина, то мы можем считать 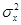 известной константой, а математическое ожидание
известной константой, а математическое ожидание 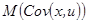 равным нулю. Тогда:
равным нулю. Тогда:
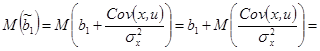
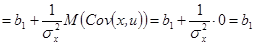 .
.
То есть 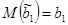 , следовательно,
, следовательно, 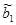 является несмещенной оценкой b1.
является несмещенной оценкой b1.
Аналогично доказывается несмещенность оценки 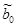 .
.
Эффективность МНК-оценок доказывается с помощью теоремы Гаусса-Маркова, которая гласит:
Метод наименьших квадратов дает оценки, имеющие наименьшую дисперсию в классе всех линейных несмещенных оценок, если выполняются предпосылки нормальной линейной регрессионной модели (см. п. 1.2.2).
Ковариационная матрица МНК-оценок параметров регрессии – матрица ковариаций оценок параметров. Для случая парной регрессии это матрица размером 2´2:
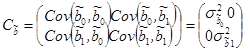 .
.
Данная матрица в соответствии с методом наименьших квадратов рассчитывается следующим образом:
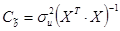 .
.
На главной диагонали данной матрицы, находятся дисперсии МНК-оценок параметров. Для случая парной линейной регрессии формулы расчета дисперсий МНК-оценок параметров следующие:
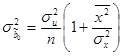 ,
, 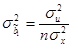 ,
,
где 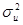 – дисперсия случайной составляющей;
– дисперсия случайной составляющей;
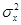 – дисперсия факторного признака x.
– дисперсия факторного признака x.
Так как 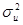 нам известна, то при расчете ковариационной матрицы пользуются оценкой дисперсии случайных составляющих –
нам известна, то при расчете ковариационной матрицы пользуются оценкой дисперсии случайных составляющих – 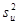 . Тогда получим оцененную ковариационную матрицу:
. Тогда получим оцененную ковариационную матрицу: 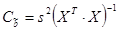 .
.
Формулы расчета оценок дисперсий 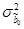 и
и 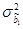 (полученные через
(полученные через 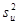 ) в случае парной линейной регрессии будут следующими:
) в случае парной линейной регрессии будут следующими:
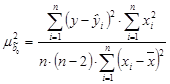 ,
, 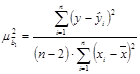
Корень из оценки дисперсии 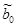 и
и 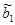 .
.
 2015-05-18
2015-05-18 6067
6067
