При оценке параметров уравнения регрессии чаще всего применяется традиционный метод наименьших квадратов. При этом должны выполняться определенные предпосылки относительно случайной составляющей ui и объясняющих переменных хi (предпосылки нормальной линейной модели). Напомним, что ui, имеет смысл отклонения в линейной модели регрессии: 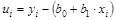 .
.
Третья предпосылка гласит: 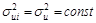 , i=1;n, что означает постоянство дисперсий случайных составляющих для каждого наблюдения i.
, i=1;n, что означает постоянство дисперсий случайных составляющих для каждого наблюдения i.
Поясним данную предпосылку на примере. Случайная составляющая ui в каждом наблюдении может иметь только одно значение. Что же означает дисперсия ui? Имеется в виду возможное поведение ui до того, как проведено наблюдение. То есть нет основания apriori ожидать появления особенно больших отклонений в любом наблюдении i=1;n. Иными словами вероятность того, что величина ui примет какое-то данное значение, будет одинакова для всех i. Это условие известно как условие гомоскедастичности, что означает одинаковый разброс.
Вместе с тем, для некоторых выборок можно предположить, что теоретическое распределение случайной составляющей ui является различным для разных наблюдений в выборке, а следовательно, различными будут и дисперсии случайных составляющих. Если дисперсии случайных составляющих неодинаковы в разных наблюдениях: 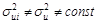 , i, j = 1;n (i ¹ j), говорят, что имеет место гетероскедастичность (т. е. неодинаковый разброс случайных составляющих). Например, если исследуется зависимость расходов на питание в семье от ее общего дохода, то можно ожидать, что разброс данных будет выше для семей с более высоким доходом. Это означает, что дисперсии зависимых величин – расходов на питание, (а следовательно, и случайных ошибок) не постоянны для отдельных значений объясняющей переменной – дохода.
, i, j = 1;n (i ¹ j), говорят, что имеет место гетероскедастичность (т. е. неодинаковый разброс случайных составляющих). Например, если исследуется зависимость расходов на питание в семье от ее общего дохода, то можно ожидать, что разброс данных будет выше для семей с более высоким доходом. Это означает, что дисперсии зависимых величин – расходов на питание, (а следовательно, и случайных ошибок) не постоянны для отдельных значений объясняющей переменной – дохода.
Гетероскедастичность может иметь место и при использовании в качестве данных наблюдений временных рядов (хt, уt). Если значения хt и уt увеличиваются со временем, то, возможно, и дисперсия случайной составляющей также будет расти со временем.
Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 2.2).
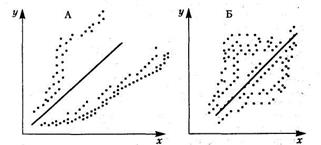
Рис. 2.2. Корреляционное поле. Случаи гетероскедастичности
На рис. 2.2, а дисперсия случайных составляющих растет по мере увеличения х. На рис. 2.2, б дисперсия случайных составляющих достигает максимальной величины при средних значениях х и уменьшается при минимальных и максимальных значениях х.
Кроме того, наличие гетероскедастичности можно проследить из графика зависимости остатков еi от расчетного значения признака-результата 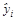 . Гетероскедастичность, соответствующая полю корреляции а на рис. 2.2, приведена на рис. 2.3, а, гетероскедастичность, соответствующая полю корреляции б на рис. 2.2, приведена на рис. 2.3, б.
. Гетероскедастичность, соответствующая полю корреляции а на рис. 2.2, приведена на рис. 2.3, а, гетероскедастичность, соответствующая полю корреляции б на рис. 2.2, приведена на рис. 2.3, б.
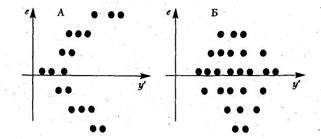
Рис. 2.3. Графики зависимости остатков от теоретических значений результата.
Случаи гетероскедастичности
Последствия гетероскедастичности:
- оценки параметров уравнения регрессии становятся неэффективными;
- оценки стандартных ошибок параметров регрессии будут неверными. (Например, оценки стандартных ошибок могут оказаться заниженными. Тогда значения t -критерия окажутся завышенными. Мы решим, что параметр регрессии значим, а на самом деле это будет не так. То есть могут быть получены неверные выводы о надежности уравнения регрессии.)
Обнаружение гетероскедастичности. Наиболее популярным является тест Голдфелда-Квандта.
Данный тест используется для проверки следующего типа гетероскедастичности: когда среднее квадратическое отклонение случайной составляющей 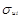 пропорционально значению признака-фактора хi в i -м наблюдении. При этом делается предположение, что случайная составляющая ui распределена нормально.
пропорционально значению признака-фактора хi в i -м наблюдении. При этом делается предположение, что случайная составляющая ui распределена нормально.
Алгоритм-тест Голдфелда-Квандта приведен ниже.
Все наблюдения i = 1; n упорядочиваются по значению xi.
Оценивается регрессия: 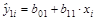 (i = 1; n ‘) для первых n' наблюдений.
(i = 1; n ‘) для первых n' наблюдений.
Оценивается регрессия: 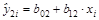 (i = n –(n’ + 1); n) для последних n' наблюдений. (n' < n/2).
(i = n –(n’ + 1); n) для последних n' наблюдений. (n' < n/2).
Рассчитывают суммы квадратов отклонений фактических значений признака-результата от его расчетных значений для обеих регрессий:
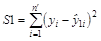 и
и 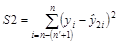 .
.
Находят отношение сумм квадратов отклонений: S1/S2 (или S2/S1). В числителе должна быть наибольшая из сумм квадратов отклонений. Данное отношение имеет F -распределение со степенями свободы: k1=n’-h и k2=n’-h, где h – число оцениваемых параметров в уравнении регрессии.
Если 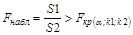 , то гетероскедастичность имеет место.
, то гетероскедастичность имеет место.
Если в модели более одного фактора, то наблюдения должны упорядочиваться по тому фактору, который, как предполагается, теснее связан с 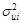 , и n’ должно быть больше, чем h.
, и n’ должно быть больше, чем h.
Устранение гетероскедастичности. Для этого нужно найти способ придать наибольший вес наблюдению i, у которого среднее квадратическое отклонение случайной составляющей 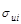 максимально (такие наблюдения обладают самым низким качеством); и малый вес наблюдению, у которого среднее квадратическое отклонение случайной составляющей
максимально (такие наблюдения обладают самым низким качеством); и малый вес наблюдению, у которого среднее квадратическое отклонение случайной составляющей 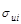 минимально (такие наблюдения обладают самым высоким качеством). Тогда мы получим более точные (эффективные) оценки параметров уравнения регрессии:
минимально (такие наблюдения обладают самым высоким качеством). Тогда мы получим более точные (эффективные) оценки параметров уравнения регрессии: 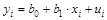 .
.
Разделим правую и левую части уравнения на 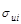 . Получим:
. Получим: 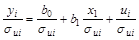 .
.
Введем новые переменные:
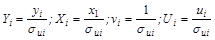 .
.
Тогда уравнение регрессии примет вид:
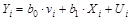 .
.
Преобразованное уравнение относится к двухфакторному уравнению регрессии (1-й фактор – X, 2-й фактор — v). Данное уравнение представляет собой так называемую взвешенную регрессию (с весами 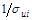 ). При этом наблюдениям высокого качества с меньшими
). При этом наблюдениям высокого качества с меньшими 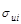 придаются большие веса
придаются большие веса 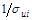 и наоборот. Случайная составляющая в i -м наблюдении –
и наоборот. Случайная составляющая в i -м наблюдении – 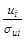 имеет постоянную дисперсию:
имеет постоянную дисперсию:
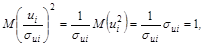
т. е. модель будет гомоскедастичной.
Данный способ устранения гетероскедастичности применим, если известны фактические значения 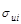 , что не встречается на практике.
, что не встречается на практике.
Однако, если мы сможем подобрать некоторую величину, пропорциональную 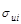 в каждом наблюдении i = 1; n, и разделим на нее обе части уравнения, то гетероскедастичность будет устранена. Например, может оказаться целесообразным предположить, что
в каждом наблюдении i = 1; n, и разделим на нее обе части уравнения, то гетероскедастичность будет устранена. Например, может оказаться целесообразным предположить, что 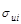 приблизительно пропорциональна xi, как в критерии Голдфелда-Квандта
приблизительно пропорциональна xi, как в критерии Голдфелда-Квандта 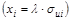 .
.
Тогда: 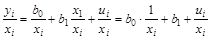 .
.
Если «повезет», новая случайная составляющая 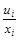 будет иметь постоянную дисперсию. Оценим регрессию новой зависимой переменной
будет иметь постоянную дисперсию. Оценим регрессию новой зависимой переменной 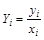 на новую независимую переменную
на новую независимую переменную 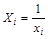 . Тогда коэффициент при этой переменной – эффективная оценка параметра b0, а постоянный член – эффективная оценка параметра b1 исходного уравнения регрессии:
. Тогда коэффициент при этой переменной – эффективная оценка параметра b0, а постоянный член – эффективная оценка параметра b1 исходного уравнения регрессии: 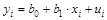 . Дисперсия случайной составляющей в этом уравнении может быть записана как
. Дисперсия случайной составляющей в этом уравнении может быть записана как
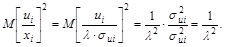
То есть она будет постоянна для всех наблюдений. Следовательно, гетероскедастичность в преобразованном уравнении регрессии отсутствует.
 2015-05-18
2015-05-18 1544
1544








