Обобщенный метод наименьших квадратов (ОМНК) применяется в том случае, если нарушена третья, либо четвертая предпосылки нормальной линейной регрессионной модели, т. е. если случайные составляющие не имеют постоянной дисперсии или коррелированны между собой. Это характерно для неоднородной совокупности, состоящей из сильно отличающихся друг от друга единиц.
В этом случае имеет место обобщенная линейная модель множественной регрессии, которая в матричной форме выглядит так:
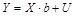 .
.
X – неслучайная матрица, имеющая полный ранг, т, е. х1, х2,..., хm – неслучайные переменные.
М(U) = 0.
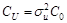 , где С0 – некоторая заранее известная матрица.
, где С0 – некоторая заранее известная матрица.
Основное отличие обобщенной регрессионной модели от нормальной состоит в виде матрицы ковариации случайных составляющих – СU. В нормальной модели предполагается, что матрица С0 равна единичной матрице. В обобщенной модели допускается, что ковариации (следовательно, дисперсии и корреляции) остатков могут быть произвольными, следовательно, и матрица С0 может содержать произвольные значения. В этом – суть обобщения нормальной модели.
Применение традиционного (обычного) МНК к обобщённой регрессионной модели дает состоятельные и несмещенные оценки. Однако данные оценки становятся неэффективными. Поэтому для оценивания параметров обобщенной модели пользуются обобщенным МНК. При этом вектор оценок параметров модели определяется по формуле:
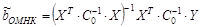 (2.8)
(2.8)
Следует отметить, что для обобщенной регрессионной модели, в отличие от нормальной, коэффициент детерминации R2 не может служить удовлетворительной мерой качества модели. Он даже не обязан лежать в интервале от 0 до 1, а добавление или удаление независимой переменной не обязательно приводит к его увеличению или уменьшению.
Проверка гипотез о значимости коэффициентов регрессии проводится так же, как и в случае нормальной линейной модели.
Ковариационная матрица МНК-оценок параметров регрессии (которая используется для определения дисперсий и стандартных ошибок оценок параметров) будет рассчитываться как 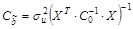 .
.
В отличие от нормальной модели регрессии 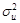 , уже нельзя интерпретировать как величину дисперсии случайной составляющей. Однако для получения ковариационной матрицей МНК-оценок ее нужно оценить. Для этого используют следующую формулу:
, уже нельзя интерпретировать как величину дисперсии случайной составляющей. Однако для получения ковариационной матрицей МНК-оценок ее нужно оценить. Для этого используют следующую формулу:
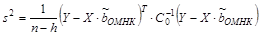 .
.
Для применения ОМНК необходимо знать матрицу СU, что на практике бывает редко. Рекомендуется оценить каким-либо образом матрицу СU, а затем использовать эту оценку в формуле (2.8) вместо С0. Для этого вводят априорные ограничения на структуру матрицы СU. Данный подход составляет суть так называемого доступного обобщенного метода наименьших квадратов (FGLS) и используется при оценивании параметров в модели с гетероскедастичностью, а также в случае автокорреляции случайных составляющих.
Рассмотрим ковариационную матрицу случайных составляющих в случае их гетероскедастичности и взаимной независимости; Если предположить, что 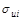 приблизительно пропорциональна хi т.е.
приблизительно пропорциональна хi т.е. 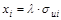 , то ковариационная матрица может быть представлена в виде:
, то ковариационная матрица может быть представлена в виде:
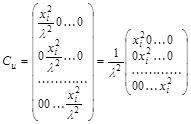 .
.
Рассмотрим ковариационную матрицу случайных составляющих в случае их автокорреляции. При сохранении свойства гомоскедастичности и в предположении, что случайные составляющие связаны автокорреляционной зависимостью 1-го порядка: 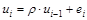 , ковариационная матрица может быть представлена в виде:
, ковариационная матрица может быть представлена в виде:
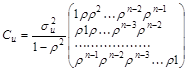 ,
,

 где
где 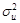 – дисперсия случайной составляющей, оценкой которой служит величина:
– дисперсия случайной составляющей, оценкой которой служит величина:
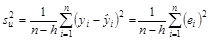 ,
,
где h – число оцениваемых параметров;
n – объем выборки.
 2015-05-18
2015-05-18 2327
2327