Оценка точно идентифицированного уравнения. Косвенный метод наименьших квадратов (КМНК – ILS)

Оценка точно идентифицированного уравнения осуществляется с помощью косвенного метода наименьших квадратов (КМНК).

Алгоритм КМНК включает 3 шага:

1. составление приведенной формы модели и выражение каждого коэффициента приведенной формы через структурные параметры;

2. применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приведенных параметров;

3. определение оценок параметров структурной формы по оценкам приведенных коэффициентов, используя соотношения, найденные на 1-м шаге.

Примечание: при небольшом числе переменных можно не определять приведенные коэффициенты через структурные параметры, что приводит к необходимости решения нелинейной системы уравнений, а воспользоваться более простым приемом – получить из имеющихся приведенных уравнений структурные уравнения.

Рассмотрим пример. Пусть дана структурная форма модели спроса и предложения:

;

.

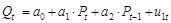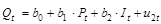В данной модели эндогенными переменными (т.е. определяемыми внутри модели) являются взаимозависимые переменные: Р_t – цена; Q_t –количество товара.

• предопределенными переменными (которые определяют значения эндогенных переменных) являются:

I_t – доход (экзогенная переменная);

Р_t-1 – цена в предыдущий период времени (лаговая эндогенная переменная);

• случайными переменными являются: u_1t, u_2t;

• структурными параметрами модели являются:
a₀, a₁, a₂, b₀, b₁, b₂.

Имеются данные за 6 периодов времени по переменным (табл. 2.7).

Таблица 2.7

t	Qt	Рt	It	Рt-1
Итого

Найдем оценки структурных параметров модели.

Ранее было показано, что данная модель точно идентифицирована.

Поэтому для оценки структурных параметров модели можно применить косвенный МНК:

1 шаг. Составим приведенную форму:

;

.

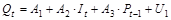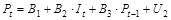2 шаг. С помощью обычного МНК найдем оценки приведенных коэффициентов. В соответствии с методикой МНК, система нормальных уравнений для расчета параметров 1-го приведенного уравнения (А₁, А₂, А₃) примет вид:

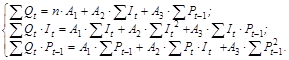
По данным табл. 11 имеем:

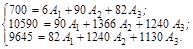
Решив систему находим, что A₁ = 1,55; А₂ = 1,15;
А₃ = 7,16.

Аналогично определяем параметры 2-го приведенного уравнения (В₁, В₂, В₃).

Окончательно оцененная приведенная форма модели имеет вид:

;

.

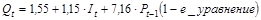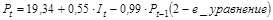3 шаг. По оцененной приведенной форме получим 1-е уравнение структурной формы модели – зависимость Q_t от Р_t и Р_t-1. Для этого выразим из 2-го уравнения приведенной формы I_t:

I_t = –19,34/0,55+(0,99/0,55) Р_t-1+(1/0,55)Р_t =
= –34,9+1,78 Р_t-1 +1,8 Р_t.

Затем подставим полученное выражение в 1-е уравнение приведенной формы:

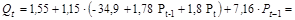
=–38,54+2,07 Р_t +9,21 Р_t-1.

Следовательно, а₀ = 38,54; а₁ = –2,07; а₂ =–9,21.

Аналогично можно определить параметры 2-го Структурного уравнения, представляющего собой зависимость Q_t от Р_t и I_t. Для этого выразим из 2-го уравнения приведенной формы Р_t-1:

Р_t-1 =19,34/0,99 + (0,55/0,99) I_t – (1/0,99) Р_t =
=19,6 + 0,56 I_t –1,01 Р_t.

Затем подставим полученное выражение в 1-е уравнение приведенной формы:

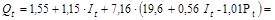
=141,95–7,26 Р_t +5,17 I_t.

Следовательно, b₀ =141,95; b₁ = –7,26; b₂ = 5,17.

В результате структурная форма модели имеет вид:

Q_t =–38,54+2,07 Р_t +9,21 Р_t-1 R² = 0,923;

Q_t =141,95–7,26 Р_t +5,17 I_t R² = 0,77.

Для сравнения обычный МНК дает следующие результаты:

Q_t =5,2–0,166 Р_t +8,33 Р_t-1 R² = 0,962;

Q_t =90,38–3,85 Р_t +5,38 I_t R² = 0,887.

Это смещенные оценки структурных параметров модели.

2.5.3. Оценка сверхидентифицированного уравнения.
Двухшаговый метод наименьших квадратов (ДМНК – 2 SLS)

Оценка сверхидентифицируемого уравнения осуществляется при помощи двухшагового метода наименьших квадратов (ДМНК – 2 SLS).

Алгоритм двухшагового МНК включает следующие шаги:

1) составление приведенной формы модели;

2) применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приведенных параметров;

3) определение расчетных значений эндогенных переменных, которые фигурируют в качестве факторов в структурной форме модели;

4) определение структурных параметров каждого уравнения в отдельности обычным МНК, используя в качестве факторов входящие в это уравнение предопределенные переменные и расчетные значения эндогенных переменных, полученные на шаге 1.

Параметры сверхидентифицированной функции предложения нельзя определить косвенным МНК. Обычный МНК также нельзя применять, так как в этом случае были бы нарушены предпосылки нормальной линейной модели регрессии. Нарушение этих предпосылок связано с наличием в уравнении в качестве фактора эндогенной переменной у_t.

Предположим, что мы нашли переменную 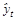, которая имеет 2 свойства:

• тесно коррелирует с переменной у_t;

• не коррелирует со случайной составляющей.

Такие переменные в эконометрике называются инструментальными переменными. Они отвечают предпосылкам нормальной линейной регрессионной модели.

Если мы теперь заменим в уравнении регрессии переменную у_t (выступающую в роли фактора) инструментальной переменной 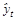, то к такому преобразованному уравнению регрессии можно применить обычный МНК.

Рассмотрим пример. Вернемся к модели спроса и предложения (см. п.2.5.2) и введем новую предопределенную переменную R_t – благосостояние потребителей в уравнение спроса:

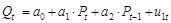– функция предложения;

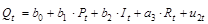– функция спроса.

Исходные данные приведены в табл. 2.8.

Таблица 2.8

t	Qt	Рt	It	Рt-1	Rt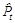
						14,85
						12,23
						14,05
						15,20
						13,57
						15,10
Итого

Найдем оценки параметров структурной формы модели.

В этой модели функция спроса точно идентифицирована, а функция предложения сверхидентифицирована; при этом выполняется достаточное условие идентификации.

Параметры сверхидентифицированной функции предложения нельзя определить косвенным МНК. Обычный МНК также нельзя применять, т. к. в этом случае были бы нарушены предпосылки применения этого метода. Нарушение этих предпосылок связано с наличием в уравнении в качестве фактора эндогенной переменной Р_t.

Используем двухшаговый МНК для оценок параметров уравнения предложения.

1 шаг. Выпишем приведенную форму модели:

;

.

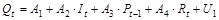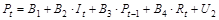Из второго уравнения модели можно найти расчетные значения :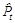

.

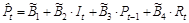Второе уравнение приведенной формы можно переписать в виде:

.

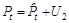Таким образом, переменная Р_t состоит из двух элементов:

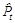• , которая есть линейная комбинация преопределенных переменных (I_t, R_t-1 и R_t);

• U₂, которая в соответствии с предпосылкой МНК не коррелирует с переменной .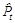

Сверхидентифицированную функцию предложения можно переписать в виде:

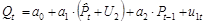или

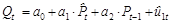
где .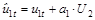

Полученное уравнение отличается от исходной функции предложения только тем, что переменная Р_t заменена на ее оценку 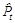, и ошибкой .

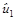Переменная 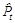имеет следующие свойства:

1) она тесно коррелирует с Р_t;

2) она не коррелирует с ошибкой .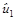

Таким образом, она является инструментальной переменной.

2 шаг. Определим обычным МНК параметры приведенной формы модели, используя данные таблицы 2.8:

;

.

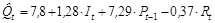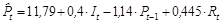4 шаг. Подставим во 2-е уравнение приведенной формы фактические значения I_t, R_t-1, R_t из таблицы, найдем расчетные значения 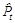и добавим их в табл. 2.8.

Например 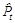= 11,79 + 0,4 × 14 - 1,14 × 12 + 0,445 × 25 = 14,85.

5 шаг. Применим обычный МНК к уравнению:

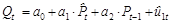
В результате получим:

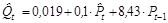R² = 0,962;

Таким образом, структурные параметры уравнения предложения найдены.

Параметры точно идентифицированной функции спроса можно определить двумя способами:

Двухшаговым МНК:

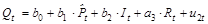
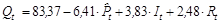R² = 0,976.

Косвенным МНК (т.к. функция спроса точно идентифицирована).

Для этого выразим из 2-го уравнения приведенной формы переменную
Р_t-1:

Р_t-1 = 10,37 – 0,88 × Р_t + 0,35 × I_t + 0,39 × R_t.

Подставим найденное выражение вместо Р_t-1 в 1-е уравнение приведенной формы и получим:

Q_t =83,37 – 6,41 × Р_t + 3,83 × I_t + 2,48 × R_t.

Это 2-е уравнение структурной формы, параметры которого найдены КМНК.

Выпишем структурную форму модели:

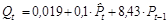R² = 0,962.

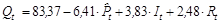R² = 0,976.

Для сравнения обычный МНК дает следующие результаты:

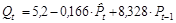R² = 0,962.

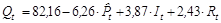R² = 0,983.

!

Хотя функция предложения по сравнению с предыдущей моделью, в которую не входила переменная R_t не изменилась, оценки ее структурных параметров изменились, т.к. изменилась вся модель: в нее была включена дополнительная предопределенная переменная. А обычный МНК не привел бы к изменению оценок структурных параметров функции.

Выделим 3 главные особенности двухшагового МНК.

1. Двухшаговый МНК может применяться для оценки не только сверхидентифицированных, но и точно идентифицированных уравнений. В этом случае оценки, полученные двухшаговым и косвенным МНК, совпадут.

2. Если значения коэффициентов детерминации по у нениям приведенной формы велико и превышает 0,8 (R² > 0,8), то оценки структурных параметров, полученные двухшаговым и обычным МНК, будут близки. Причина в том, что при высоком R² расчетные значения инструментальных переменных не будут сильно отличаться от фактического значения соответствующих эндогенных переменных.

1. Однако если коэффициент детерминации R² для приведенного уравнения низкий, то расчетные значения эндогенной переменной будут плохой аппроксимацией ее фактических значений и применение двухшагового МНК может оказаться неэффективным.

Тесты по разделу

Из перечисленных условий: 1) большое число наблюдений, 2) незначительное число наблюдений, 3) маленькие выборочные дисперсии объясняющих переменных, 4) большие выборочные дисперсии объясняющих переменных, 5) большая дисперсия случайного члена, 6) малая дисперсия случайного члена - к условиям, благоприятствующим получению надежных оценок регрессии, относятся

a) 2,3,5

b) 1,3,5

c) 2,4,6

d) 1,4,6